Symmetries of graphs/Graph theory

[CAF123]

Homework Statement

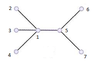
Determine the number of symmetries of the graph attached.

The Attempt at a Solution

I know the answer, I would just like someone to look over my argument to make sure I haven't missed out anything important. I also have some questions along the way.

Vertex 1 is the only vertex with valency 4 and so by defintion, symmetries preserve valancy, therefore any symmetry must leave vertex 1 in place.
Given that 1 is fixed, 2,3,4 must be attached to 1, but they need not be in the same position, so there are 3! permutations of these three vertices. (First question: How can I be sure that it is definitely 3!? I know the symmetries of a graph are independent on the way you draw it, so would there not be a chance that two of such permutations might actually correspond to the same permutation. The answer is probably no, but it is not that obvious to me.)

Similarly vertex 5 has valence 3 so it must be fixed and by same reasoning above 2! permutations of 6 and 7. Total number of symmetries = 3! . 2! = 12.
(2nd Question: Is the distribution of vertices 2,3,4 independent of that of 6,7. I.e if I send 2 to 3 then does that mean anything for what happens to 6 on the other side, for example? I feel the answer is no, but this is completely against what a symmetry would mean in a non-mathematical context. Is it correct to say that a symmetry in mathematics is not the same as a the notion of symmetry I would have had before I took this class?

(Last Question: Is it possible to say what these symmetries are? I.e one is the identity, one I think reflection, and the rest just rotations)

Many thanks

 

[haruspex]

How can I be sure that it is definitely 3!?

Imagine you have two copies of the graph. You can map vertex 2 in one copy to any of the three in the other copy, and whichever you map it to you still have two choices for where to map vertex 3.

Is the distribution of vertices 2,3,4 independent of that of 6,7. I.e if I send 2 to 3 then does that mean anything for what happens to 6 on the other side, for example? I feel the answer is no, but this is completely against what a symmetry would mean in a non-mathematical context. Is it correct to say that a symmetry in mathematics is not the same as a the notion of symmetry I would have had before I took this class?

Is it possible to say what these symmetries are? I.e one is the identity, one I think reflection, and the rest just rotations)

Yes, (234) is quite independent of (67). These are not geometric symmetries, so don't think of them as reflections and rotations. Permutations, yes.

 

[CAF123]

Imagine you have two copies of the graph. You can map vertex 2 in one copy to any of the three in the other copy, and whichever you map it to you still have two choices for where to map vertex 3.

Yes, (234) is quite independent of (67). These are not geometric symmetries, so don't think of them as reflections and rotations. Permutations, yes.

Ok, thanks. So we don't speak about rotations/reflections in this case? When do we speak about rotations/reflections ? every symmetry (at least what i have done) is considered a permutation of the points but I do recall speaking about rotations/reflections for this type of graph before in my class also (I.e some permutation of points corresponds to a reflection, say) and also for the symmetries of the ngons.

 

[haruspex]

For C_n graphs, it's sort of reasonable to map them to n-agons and discuss symmetries geometrically, though I struggle to put into words exactly why that is. But it can get quite misleading with more complicated graphs, e.g. K_3,3. There can be quite different-looking presentations of a graph in the plane (especially non-planar ones!), so what might look like a reflection in one presentation might look quite different in another.

 

[CAF123]

I haven't covered anything like K_3,3 before. My course is introductory group theory. I thought that I could say, for example, since we fix 1 and 5, and then say swap 3 with 4, 4 with 3 and 6 with 7, 7 with 6 this should correspond to a reflection? Is this correct? Would I then be right in saying that the rest (apart from identity) correspond to rotations?
EDIT: one thing I forgot to ask was why is that if 1 is fixed, 2,3,4 have to stay attached to 1 after some permutation? I don't see this anywhere in the defintion I have. (I have sort of took it for granted up to now)
Thanks

 

[haruspex]

I since we fix 1 and 5, and then say swap 3 with 4, 4 with 3 and 6 with 7, 7 with 6 this should correspond to a reflection?

I'm guessing you meant 'swap 2 with 4 and 6 with 7'. That certainly looks like a reflection in the diagram, but you have to distinguish between the graph as an abstract mathematical structure (which is where the automorphisms operate) and a specific drawing of it. In the abstract view, swapping 2 with 4 is no different in nature from swapping 3 with 4, and there's certainly nothing special about swapping 2 with 4 at the same time as swapping 6 with 7

Is this correct? Would I then be right in saying that the rest (apart from identity) correspond to rotations?

Not really. "Rotation" still has a geometrical feel to it. In terms of group structure, it's S3xS2.

EDIT: one thing I forgot to ask was why is that if 1 is fixed, 2,3,4 have to stay attached to 1 after some permutation? I don't see this anywhere in the defintion I have. (I have sort of took it for granted up to now)

Automorphisms of graphs by definition preserve adjacency. If 1 is fixed then a vertex adjacent to 1 can only be mapped to another vertex adjacent to 1. Suppose we delete vertex 4. Now 1 and 5 look the same, so can be swapped. If an automorphism does that then it must also swap the pair 2, 3 with the pair 6, 7.

 

[CAF123]

"Rotation" still has a geometrical feel to it. In terms of group structure, it's S3xS2.

Strange.. We have been talking about rotations/reflections for these types of planar graphs in class.

 

[haruspex]

Strange.. We have been talking about rotations/reflections for these types of planar graphs in class.

Oh dear.

 

[CAF123]

Should I speak to my lecturer about this?
For example, consider the 4-gon(square). We said there are eight symmetries: 4 reflections, 3 rotations and identity. Is this incorrect?
Similarly, we discussed rotations/reflections for planar graphs etc... perhaps he was doing this for us to get a feel for what we are doing... But then again, as I have learned, the mathematical notion of a symmetry is very different from that of everyday life.

 

[haruspex]

As I said, you can get away with that for simple circuit graphs (C_n). But consider e.g. K_2,3, which you might draw as a square with a point in the middle, the central point being connected to two diametrically opposite corners. In the drawn version, you would see two reflections and a 180 degree rotation, leading to a group S2xS2. But as a graph, the three vertices of degree 2 are completely equivalent, so the group is S2xS3.