mananvpanchal said:
- You are using TD equation to find time readings, that is wrong. I agree that time dilation difference between two readings of each three clocks are same for R. But time readings of each three clocks are not same for R. To find time reading you have to use LT equation.
Not only is my use of the equation correct, I proved that it is correct from first principles, the spacetime interval equation.
The Lorentz
transform is used to
transform from the unprimed frame to the primed frame, it is not useful within a single frame. It is always used, once you have completely specified the problem in one frame, to determine how the problem appears in any other frame.
The LT cannot be used to specify the problem within a single frame. You should have realized that you were making a mistake when your use of the LT contradicted your initial scenario.
mananvpanchal said:
- You are telling \tau is not dependent of d, and you have proved forcefully that clocks is synchronized for R using TD equation and using single independent value of \tau. But then you have a goal to prove that clocks is not synchronized for O. So, you came up with three values of \tau. But, how could you not realize that if \tau is not dependent of d then how could you get three values of \tau? And if there are three values of \tau exist then how could you prove that clocks is synchronized for R using the TD equation?
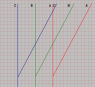
This is a valid point. My apologies for the confusion. There are always 3 values of τ in both frames. So I should have written:
for \tau_d>0
(\tau_d - 0)^2 = (t-0)^2 - ((0.6t+d) - (0 + d))^2
\tau_d = 1.25 t
Where \tau_a, \tau_o, \tau_b are found by substituting the appropriate values of d into the equation.
Is that more clear?
mananvpanchal said:
- You said my modified diagram (modified by you) shows that clocks is not synchronized for O. Then how does the modified diagram shows that clocks is synchronized for R?
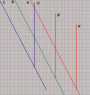
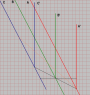
First, do you agree that the clocks each read 0 at the black dots in your scenario?
If so, then along each worldline simply find points of equal spacetime interval from the black dots and note that they occur simultaneously for R.
If not, then please mark where each clock reads 0 clearly on your diagram.
mananvpanchal said:
- I cannot understand that why you don't want to understand this: If a clock is at rest in a frame then its proper time (what time interval it has covered in the frame) is equal to co-ordinate time of the frame (because covered space interval is zero in the frame).
Again, my watch and my desk clock are both at rest in my frame, and they have different readings of proper time. One says 1:19 and the other says 1:21. So it is not possible for them to both be equal to the co-ordinate time. They are not synchronized. This disproves your claim by counterexample.
You are focusing on the fact that they are running at the same rate as coordinate time in my frame. However, that is not relevant to determining synchronization. Two clocks may be running fast or slow and yet be synchronized. They may be running at the correct rate and yet not be synchronized. You are mixing two separate concepts.
mananvpanchal said:
- I cannot understand that why you don't want to understand this: Line of simultaneity is the line on which, two events occurred, called simultaneous events. So short hand and long hand of clocks on the line meets at 12 must be simultaneous events on the line of simultaneity. So clocks on the line can be called synchronized. If clocks on line of simultaneity is not synchronized then what is other method you have to prove that two events occurred on the line of simultaneity is simultaneous events?
You are again confusing simultaneity with synchronization. Simply because you can draw a line of simultaneity on a spacetime diagram does not imply that all clocks will read the same on that line of simultaneity unless the clocks are synchronized.
The procedure for synchronization was given by Einstein. In your problem setup you stated that the clocks were initially synchronized in the unprimed frame. Meaning that Einstein's procedure synchronization procedure was carried out initially.
Because the clocks were synchronized in the unprimed frame, and because their velocity profile is the same in the unprimed frame at all times, they remain synchronized in the unprimed frame, as I proved. Because they are synchronized in the unprimed frame, they are not synchronized in the primed frame frame, as I proved.
mananvpanchal said:
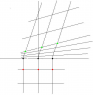
- Accelerating scenario can be made up using too many small inertial frames changing. My diagram shows how lines of simultaneity of O's frame becomes unparallel to space axis of R's frame (during acceleration and after acceleration). So, clocks on the lines of simultaneity becomes desynchronized for R. But, lines of simultaneity is always parallel to space axis of whatever small inertial frame in which O exist at that time. So, clocks on the lines of simultaneity remain synchronized for O.
No they don't. Look at the gaps between your "sweeping" lines of simultaneity.
Do those gaps look like they are marking equal spacetime intervals for each clock? Please answer this question in bold directly.
mananvpanchal said:
- I have proved that train's clocks is synchronized for O and not synchronized for R using diagram and maths (LT equation).
No you haven't. You first drew physically impossible diagrams, then you misinterpreted your own diagrams. Your math is incorrect because you tried to use a transform to specify a problem rather than to transform it into a new reference frame.