Vishera
- 72
- 1
Question:
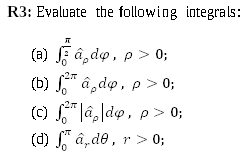
Solution:
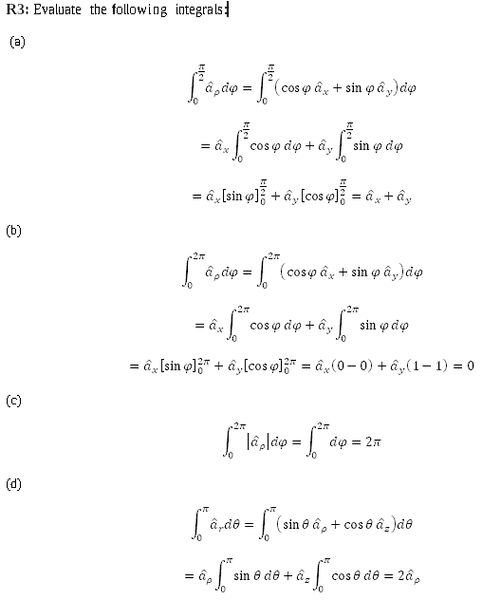
The notation used is: ##(x,y,z)## is for rectangular coordinates, ##(\rho,\varphi,z)## for cylindrical coordinates and ##(r,\theta,\varphi)## for spherical coordinates. ##{ { \hat { a } } }_{ ρ }## represents the unit vector for ##\rho## (same applies to ##x, y, z## and other coordinates).
In part a, can't you take out ##{ { \hat { a } } }_{ ρ }## from the integral? I'm having trouble understanding how ##{ { \hat { a } } }_{ ρ }## depends on ϕ. ##{ { \hat { a } } }_{ ρ }## is defined as ρ=1, ϕ=0 and z=0. Aren't all of these constants that do not rely on ϕ?
Solution:
The notation used is: ##(x,y,z)## is for rectangular coordinates, ##(\rho,\varphi,z)## for cylindrical coordinates and ##(r,\theta,\varphi)## for spherical coordinates. ##{ { \hat { a } } }_{ ρ }## represents the unit vector for ##\rho## (same applies to ##x, y, z## and other coordinates).
In part a, can't you take out ##{ { \hat { a } } }_{ ρ }## from the integral? I'm having trouble understanding how ##{ { \hat { a } } }_{ ρ }## depends on ϕ. ##{ { \hat { a } } }_{ ρ }## is defined as ρ=1, ϕ=0 and z=0. Aren't all of these constants that do not rely on ϕ?