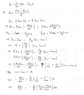PaxFinnica96
- 14
- 0
Hi All,
I'm really struggling with the below question - I'm not sure if I've taken the correct approach to determining the model as there may be an easier way to do this?
Any help in much appreciated, please let me know if I have submitted this template correctly as this if my first time!
Cheers
1. Homework Statement
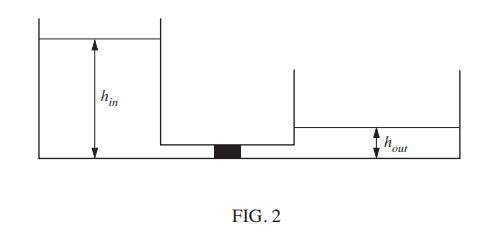
a. FIGURE 2 shows two cylindrical tanks interconnected with a pipe which has a valve that creates a constant resistance to flow of Rf when fully open. The height of liquid (of density ρ) in the first tank is hin and the second tank hout. The cross-sectional area of the first tank is Ain m2 and the second tank Aout m2.
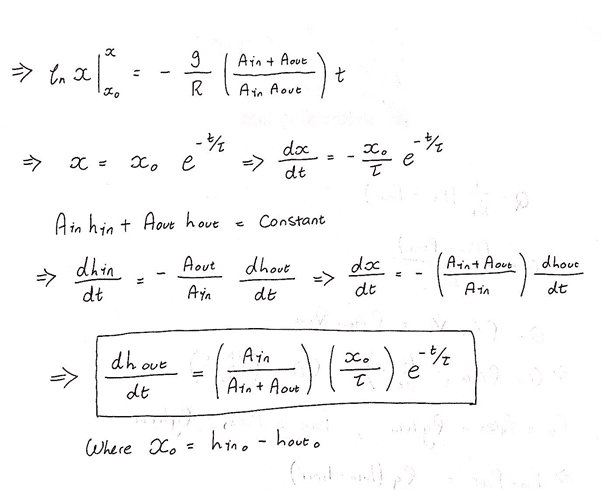
Produce a mathematical model of the process to determine the change in height of fluid in the second tank when the valve is open.
b. Determine the time constant for the system.
The flow rate of liquid through the valve is given by:[/B]
Q = 1/Rf (Pin - Pout)
Where; Q = flow rate in m^3 s^-1
Pin = pressure due to height of liquid in first tank (Pa)
Pout = pressure due to height of liquid in second tank (Pa)
a[/B]

b
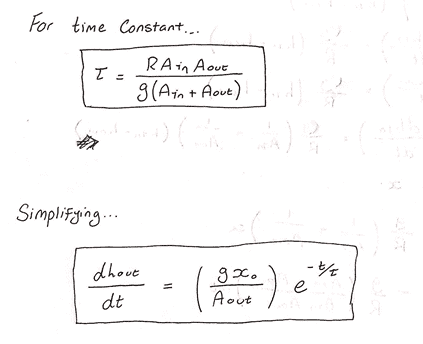
Giving a time constant of 63.2% for the system.
I'm really struggling with the below question - I'm not sure if I've taken the correct approach to determining the model as there may be an easier way to do this?
Any help in much appreciated, please let me know if I have submitted this template correctly as this if my first time!
Cheers
1. Homework Statement
a. FIGURE 2 shows two cylindrical tanks interconnected with a pipe which has a valve that creates a constant resistance to flow of Rf when fully open. The height of liquid (of density ρ) in the first tank is hin and the second tank hout. The cross-sectional area of the first tank is Ain m2 and the second tank Aout m2.
Produce a mathematical model of the process to determine the change in height of fluid in the second tank when the valve is open.
b. Determine the time constant for the system.
Homework Equations
The flow rate of liquid through the valve is given by:[/B]
Q = 1/Rf (Pin - Pout)
Where; Q = flow rate in m^3 s^-1
Pin = pressure due to height of liquid in first tank (Pa)
Pout = pressure due to height of liquid in second tank (Pa)
The Attempt at a Solution
a[/B]
b
Giving a time constant of 63.2% for the system.