SUMMARY
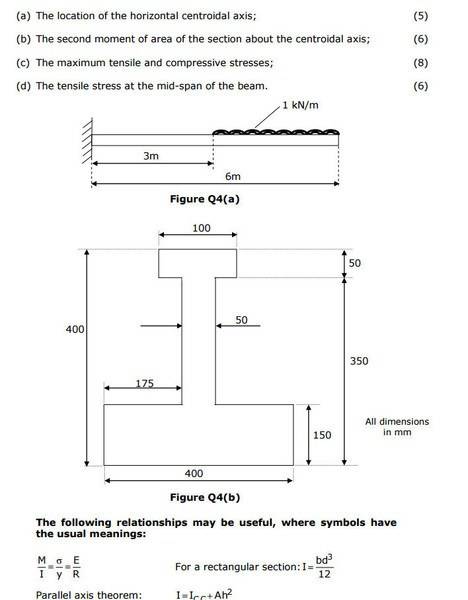
The discussion focuses on calculating the tensile stress at the mid-span of a beam, with the correct answer identified as 1.66 MPa. Key calculations involve determining the bending moment (M = 13,500 kNm) and the second moment of area (I = 762.3 x 10^6 mm^4). Participants emphasize the importance of using correct units in the formulas, specifically ensuring that M is in N-m, y in meters, and I in m^4 to obtain stress in N/m^2. The conversation also clarifies the distinction between maximum tensile and compressive stresses, with values of 4.98 MPa and 2.09 MPa, respectively.
PREREQUISITES
- Understanding of beam bending theory
- Familiarity with the formula for bending stress: σ = My / I
- Knowledge of calculating the second moment of area (I) for beam cross sections
- Ability to identify the centroidal axis of a beam cross section
NEXT STEPS
- Research the calculation of the second moment of area for various beam shapes
- Learn about the significance of the neutral axis in bending stress calculations
- Explore the effects of different loading conditions on beam stress
- Study the relationship between bending moments and shear forces in beams
USEFUL FOR
Structural engineers, civil engineering students, and professionals involved in beam design and analysis will benefit from this discussion, particularly those focused on tensile and compressive stress calculations in structural elements.