Lori
Homework Statement
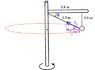
Where does T2cos(theta) come from ? Isn't mv^2/R the centripetal force which is the tension of rope 2?
Homework Equations
Fc = mv^2/R
3. Solution
Wait! The horizontal component of the circle is the centripetal force? So that part is mv^2/R?
I got confused and thought the tension of rope 2 is actually the centripetal force. But if the x point of that tension is the centripetal force, i see how they got T2Cos
since cos(theta) = Xcomp/T2
i get cos(theta) = (mv^2/R)/T2
so that T2cos(theta)= (mv^2/R)[/B]
Attachments
Last edited by a moderator: