Calgria
- 3
- 0
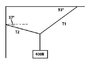
I have this tension problem that I attached and I have no idea where to start working this. We've normally just done linear things with coupled motion, either horizontally or vertically, so I'm completely lost on how to even start this. If anyone can point me in the right direction i'd appreciate it.