Jahnavi
- 848
- 102
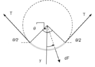
@haruspex , @kuruman If the current flows in anticlockwise direction (instead of clockwise as in the OP ) and magnetic field is perpendicular to the plane of the page , the direction of force on any infinitesimal portion of the wire will be radially inwards .
Would the force on this tiny element from the neighbouring wire element be exactly opposite to the one shown in post#11 ?
But this force doesn't look like some tension force . Is it some type of compressive force ?
But magnitude of this force will still be BIR just as in the OP .Right ?
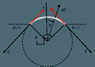
Would the force on this tiny element from the neighbouring wire element be exactly opposite to the one shown in post#11 ?
But this force doesn't look like some tension force . Is it some type of compressive force ?
But magnitude of this force will still be BIR just as in the OP .Right ?