Tension of 2 Bodies on a Frictionless Inclined Plane

[ewiner]

Homework Statement

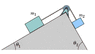
Figure 5-60 shows a box of dirty money (mass m1 = 2.7 kg) on a frictionless plane inclined at angle θ1 = 28°. The box is connected via a cord of negligible mass to a box of laundered money (mass m2 = 2.4 kg) on a frictionless plane inclined at angle θ2 = 64°. The pulley is frictionless and has negligible mass. What is the tension in the cord?

Homework Equations

F = ma

T - mgsin$$\Theta$$ = -ma

a = ( m / M + m )g

The Attempt at a Solution

Newton's 2nd law for each body:
m1: T - (2.7 kg)(9.8 m/s2)sin28 = -(2.7 kg)a
m2: (2.4 kg)(9.8 m/s2)sin68 - T = -(2.4 kg)a

Add m1 & m2: (2.4 kg)(9.8 m/s2)sin68 - (2.7 kg)(9.8 m/s2)sin28 = (2.4 + 2.7)a

Solve for a: a = 1.84

Insert a into m1: T-(2.7 kg)(9.8 m/s2)sin28 = -(2.7 kg)(1.84 m/s2)

T = 17.4 N

However, that is not the right answer... Where am I going wrong?

 

[thrill3rnit3]

Why do you have a negative sign in front of the masses? If the acceleration is negative it'll come out in your answer when you solve for a. You might be counting the negatives twice. Just my 2 cents.

 

[PhanthomJay]

Although you incorrectly threw in those negatives in front of the masses, you ignored that error and changed it correctly to a positive number when you did your equation additions and substitution to solve for T. Strange. But the other issue is that you copied the angle down incorrectly...the angle given is 64 degrees, but you used 68 degrees. Make that angle correction and solve for T using 2 significant figures in the result.

 

[thrill3rnit3]

Although you incorrectly threw in those negatives in front of the masses, you ignored that error and changed it correctly to a positive number when you did your equation additions and substitution to solve for T. Strange.

Then he went back to the negative

Insert a into m1: T-(2.7 kg)(9.8 m/s2)sin28 = -(2.7 kg)(1.84 m/s2)