Tensions in Suspended Ball System: Solving for Horizontal and Angled Cords

[EndOfMemories]

Homework Statement

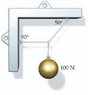
A ball weighing 100-N is shown suspended from a system of cords. What are the tensions in the horizontal and angled cords?

Homework Equations

F=ma

The Attempt at a Solution

I tried to use F=ma but I couldn't go anywhere with the equation. I know that sum of Forces (tension, gravity, normal?) equals the mass X acceleration, and there is no acceleration. So the forces equal the mass? And I got stuck here.

 

[Inferior89]

Write down the forces acting on the ball and on the cords. Split the forces you get into x and y components.

You are correct in that F = ma. And there a is 0. So F = m*0 = 0. Sum of all forces should be 0 then.

 

[rl.bhat]

Hi EndOfMemories, welcome to PF.
Let T1 be the tension in the horizontal cord and T2 be the tension in the angled cord.
Resolve T2 into vertical and horizontal components and apply the equilibrium conditions.

 

[PhanthomJay]

When an object is not in motion, there is no acceleration. Use Newton's first law in both the the y and x directions,where ax and ay are 0. . Note that tension forces always act in a direction pulling away from the object along the direction of the length of the cord, so there can be no vertical component of the tension in the horizontal cord.

 

[EndOfMemories]

Thanks guys I got it now