Terrell Revisited: The Invisibility of the Lorentz Contraction

[PAllen]

How do you derive the aberration equation?

\cos \theta_o=\frac{\cos \theta_s-\frac{v}{c}}{1-\frac{v}{c} \cos \theta_s}

You'll see I posted a quote from the wikipedia article about it from above... But the more I think about it, I start to think this might be the source of the problem in Terrell's paper.

From Wikipedia: ""the source is moving with speed

at an angle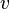

relative to the vector from the observer to the source at the time when the light is emitted. Then the following formula, which was derived by Einstein in 1905, describes the aberration of the light source, [PLAIN]http://upload.wikimedia.org/math/3/9/9/39994abba112928ccc9e9d70a502fb93.png, measured by the observer:"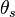

Now my reading of this is that the light is emitted along a "tube" that is aimed directly toward the observer in the reference frame of the observer when the source is at the given point.

The trouble is that if the "tube" is aimed directly toward the observer, in the reference frame of the observer, you're looking at the situation Post-Lorentz-Contraction. That is \theta_s is not the angle of the tube in the source's reference frame, but the angle of the tube in the observer's reference frame. So this equation is not relating a difference between appearances in the source's reference frame and the observer's reference frame.

Rather, it is relating a difference between two different angles measured in the observer's reference frame.

If I were to try to confirm this, I would probably try to set up a diagram similar to the one I gave in post 54, and do some vector and trigonometric calculations, dividing the velocities into well-chosen x and y components, setting the final speed of the photon through the moving tube at c, and see if I could reproduce the aberration equation from scratch.

My point is, I don't think you would find any evidence of Lorentz Contraction in the aberration equation, because the aberration equation may simply be figuring out the direction at which rays travel from already lorentz-contracted tubes.

The wikipedia description is poor. The 's' angle is measured in one reference frame, the 'o' angle is measured in the other. The discussion in the mathpages link is much clearer.

 

[harrylin]

Is it the angle of reception?

I may be misunderstanding the equation for aberration but look at the following diagram
[..] Now there's nothing wrong with the math here, insofar as it goes: [..]Now, if you're sophisticated in it enough that you've thought through all this, more power to you. [..]

Sorry in the past I was sophisticated enough to do that, but this time I imagined a simple set-up with identical emitter-receiver pairs that utilizes a basic physical principle - the laws of nature (including aberration) do not depend on position.
No math or drawings are needed (OK a mind sketch is useful) to know that if one LED shines at a certain angle, then an identical LED in an identical state must shine at the same angle, because the calculations and drawings are identical.
In the setup that I considered with identical LED's with matching CCD's, only anti-SR space anisotropy can provide a different outcome.

 

[JDoolin]

The wikipedia description is poor. The 's' angle is measured in one reference frame, the 'o' angle is measured in the other. The discussion in the mathpages link is much clearer.

Since that's a rather long page, I thought it might be helpful to focus in on what I think is the most relevant part.

I've lost my link to Terrell's paper, but I'm trying to imagine how I could use this equation to determine the shape of a relativistically passing object?

If I had an extended source which had a length L, along its velocity vector, then it is not an "object at point A" because a point cannot have a length L.

• The angle \alpha at one end of length L, would be different from the angle \alpha at the other end of length L.
• The angle \theta_s would be different at the two ends of the object.
• The time t_1 would be different at the two ends of the object.

If there is enough L there to measure length contraction, you have an object that is not located wholly at the origin, so it would become difficult, if not impossible to use any form of the aberration equation derived from having the object at the origin.

 

[Ken G]

An important thing to notice about aberration is that it is an effect that appears at order v/c, so it is primarily a simple time-of-flight effect, similar to what happens when you have directional hearing of sound waves. All we are concerned with are Lorentzian effects, i.e., that which is different in Lorentzian relativity versus Galilean relativity. Has anyone tried to calculate what a moving "plus sign" would "look like" in Galilean relativity, and compare it? I'm sure things would look pretty weird in either relativity, but we can only claim length contraction is "invisible" if what we see looks the same in both forms of relativity.

This also raises the key question: what did Terrell actually show to be true? Baez thinks he showed something really interesting to be true, and he seemed to be saying that small shapes would look the same to two observers in relative motion, but that does not seem to be true for the plus sign photographed at the instant that it appears to be at the point of closest approach for the stationary observer, because certainly the observer moving with the plus sign will never see anything but a fully symmetric plus sign. So what did Terrell prove, and did both he and Baez draw erroneous conclusions from what was actually shown?

The one thing that gives me pause is that I can't help wondering if maybe the aberration that makes the plus sign appear to be somewhere other than where it actually was when it emitted that light, means that when the stationary observer sees the light emitted when the plus sign really was at closest approach, and also sees it skewed to be shorter along the direction along its motion, aberration will make it look like it is not yet at the point of closest approach-- so they might think "oh, it's skewed because I'm seeing it from an angle that is rotated by its lateral position." Then it wouldn't "look" length contracted, it would just look rotated in a perfectly normal way and nothing relativistic would be apparent (if it was small enough).

But that doesn't sound like what Baez is saying at all-- he is saying the two photographs taken through shutters at the same time and place would photograph the same shape, so would have to be a symmetric plus sign in both, and I just can't see how that could be true. But I hesitate to conclude that something Baez has thought about this much is wrong!

 

[JDoolin]

The wikipedia description is poor. The 's' angle is measured in one reference frame, the 'o' angle is measured in the other. The discussion in the mathpages link is much clearer.

You know? I was able to confirm the equations from the mathpages link, once I understood the definitions of all the variables. It's a fairly straightforward application of the Lorentz Transformation on the vector between two events.

\begin{pmatrix} t'\\ x'\\ y' \end{pmatrix} = \begin{pmatrix} -\beta \gamma &\gamma &0 \\ \gamma &-\beta \gamma &0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} t_1\\ t_1 \cos \alpha\\ t_1 \sin \alpha \end{pmatrix}

Then the velocity angles can be calculated from x'/t', and y'/t'.

Now there's nothing wrong with the math here, insofar as it goes:

"the source is moving with speed

at an angle

relative to the vector from the observer to the source at the time when the light is emitted. Then the following formula, which was derived by Einstein in 1905, describes the aberration of the light source, [PLAIN]http://upload.wikimedia.org/math/3/9/9/39994abba112928ccc9e9d70a502fb93.png, measured by the observer:"

Although I said, before, that there is nothing wrong with the math--I should point out that it would have been incredibly difficult to guess the meaning of the 's' angle from the description given in the wikipedia article.

The angle between the source and the observer and the velocity vector "at the time the light is emitted" is NOT \theta_s.

\theta_s is the angle between the observer and the source and the velocity vector "at the time the light is received by the observer" in the source's reference frame.

 

[JDoolin]

The one thing that gives me pause is that I can't help wondering if maybe the aberration that makes the plus sign appear to be somewhere other than where it actually was when it emitted that light, means that when the stationary observer sees the light emitted when the plus sign really was at closest approach, and also sees it skewed to be shorter along the direction along its motion, aberration will make it look like it is not yet at the point of closest approach-- so they might think "oh, it's skewed because I'm seeing it from an angle that is rotated by its lateral position." Then it wouldn't "look" length contracted, it would just look rotated in a perfectly normal way and nothing relativistic would be apparent (if it was small enough).

I have been thinking today about modeling an asterisk-shaped model. A set of eight or more tubes that would show the light paths as they came out of it, as well as the Lorentz contracted moving structure.

What I'd want to show is an animation of the paths of the light following the paths predicted by the aberration equation:

(Image from http://mathpages.com/rr/s2-05/2-05.htm )

But at the same time as it shows those paths of light, it should be showing overlying simply Lorentz contracted structure of the object.

 

[A.T.]

maybe the aberration that makes the plus sign appear to be somewhere other than where it actually was when it emitted that light

The camera always sees the light coming from where it was emitted, in the rest frame of the camera.

 

[Ken G]

I have been thinking today about modeling an asterisk-shaped model. A set of eight or more tubes that would show the light paths as they came out of it, as well as the Lorentz contracted moving structure.

What I'd want to show is an animation of the paths of the light following the paths predicted by the aberration equation:

View attachment 82988
(Image from http://mathpages.com/rr/s2-05/2-05.htm )

But at the same time as it shows those paths of light, it should be showing overlying simply Lorentz contracted structure of the object.

Can you contrast a similar picture for Galilean and Lorentzian relativity? I'm wondering if the Lorentz contraction cancels out the Lorentzian modification to the aberration equation.

 

[Ken G]

The camera always sees the light coming from where it was emitted, in the rest frame of the camera.

I'm not sure that's true, wouldn't the camera see the image in the same direction that a tube would need to be pointed to accept a stream of photons from the source, not along the path of any single one of those photons? In other words, imagine a helicopter flying along a straight path, firing straight-line bullets to try to hit a single point on ground (so they have to be aimed to account for the motion of the helicopter). It seems to me the stream of bullets will arrive, at any moment, along a line that does not track the actual trajectories of the individual bullets that are coming in. If we wanted to point a tube to accept those bullets, you would have to keep the tube rotating to track the incoming bullets, and at any instant the tube would not point along the trajectory of the bullets that are hitting the bottom of the tube at that moment. So I think if the bullets are photons, the eye will see the apparent image along the direction the tube is pointing instantaneously as the photons hit the bottom, not along the direction of motion of the photons. If one takes a wavefront picture, this must have to do with how the wavefronts are turned by the phase variations coming from the movement of the source, such that we cannot expect the arriving plane wave to be perpendicular to the line from the point where the light was emitted. Is that not what aberration is?

 

[JDoolin]

I'm not sure that's true, wouldn't the camera see the image in the same direction that a tube would need to be pointed to accept a stream of photons from the source, not along the path of any single one of those photons? In other words, imagine a helicopter flying along a straight path, firing straight-line bullets to try to hit a single point on ground (so they have to be aimed to account for the motion of the helicopter). It seems to me the stream of bullets will arrive, at any moment, along a line that does not track the actual trajectories of the individual bullets that are coming in.

The bullets would arrive along many lines, each tracking the actual trajectories of the individual bullets that are coming in.

If we wanted to point a tube to accept those bullets, you would have to keep the tube rotating to track the incoming bullets, and at any instant the tube would not point along the trajectory of the bullets that are hitting the bottom of the tube at that moment.

That's a good point. The tube would have to be rotating even as it was receiving the light. If the tube were narrow enough, and the passing object were moving fast enough, you'd have to rotate the tube so fast that the photons would hit the side of the tube before they made it into the camera.

So I think if the bullets are photons, the eye will see the apparent image along the direction the tube is pointing instantaneously as the photons hit the bottom, not along the direction of motion of the photons.

Check the thumbnail. If the top of the tube is rotating to stay aligned with the incoming "bullets" the bullet arriving at the bottom is not necessarily traveling along the direction the tube is oriented.

If one takes a wavefront picture, this must have to do with how the wavefronts are turned by the phase variations coming from the movement of the source, such that we cannot expect the arriving plane wave to be perpendicular to the line from the point where the light was emitted. Is that not what aberration is?

Well, would that be consistent with the derivation I copied from http://mathpages.com/rr/s2-05/2-05.htm in post number #63? The derivation there uses the Lorentz Transformation of two events in a pair of reference frames orthogonal to the relative velocity vector of a source and an observer.

What is the principle by which we know that the Lorentz Transformation works? It is the fact that the LT is the unique transformation that preserves light-cones, while serves as an approximation for Galilean Relativity at low velocities. But at what point during all that did anyone ever say "We cannot expect the arriving plane wave to be perpendicular to the line from the point where the light was emitted?" Never. Quite the contrary, the Lorentz Transformation absolutely preserve the principle where spherical wave-fronts create images of objects at their center. That seems to me, one of the many selling-points of having a transformation which preserves the light-cone.

Now, I don't know what other people have said about the aberration equation, but, according to the derivation, I would say, yes we CAN expect the arriving plane wave to be perpendicular to the line from the point where the light was emitted.[/QUOTE]

 

[JDoolin]

Can you contrast a similar picture for Galilean and Lorentzian relativity? I'm wondering if the Lorentz contraction cancels out the Lorentzian modification to the aberration equation.

I have been thinking today about modeling an asterisk-shaped model. A set of eight or more tubes that would show the light paths as they came out of it, as well as the Lorentz contracted moving structure.

What I'd want to show is an animation of the paths of the light following the paths predicted by the aberration equation:

View attachment 82988
(Image from http://mathpages.com/rr/s2-05/2-05.htm )

But at the same time as it shows those paths of light, it should be showing overlying simply Lorentz contracted structure of the object.

Here, I just made this video showing the concept... Showing how the tubes of the source can be pointed one way in the observer's reference frame, while the actual photo paths can be pointing in an entirely different way. It's pretty sloppy, but I think, at least, it gets the idea across.

 

[A.T.]

if the bullets are photons

Light is not like bullets. If we are in flat space time and the rest frame of the camera is inertial, then light is propagating isotropically in all directions from each emission point in the rest frame of the camera, so the wave fronts reaching the static camera are perpendicular to the straight line between the camera and the emission point.

Is that not what aberration is?

There is no aberration in the rest frame of the camera.

 

[Ken G]

All right, thanks to everyone for clearing that up for me, I was definitely making aberration too difficult. My bad.

Anyway, I think I see that Baez is right, though Terrell's "invisibility" claim is still a bit of a stretch-- two cameras in relative motion that image the same object at the same place and time will always image the same shape, it will just appear to be in a different direction, and it can also have a different total angular size.

If how that could be is still as unclear to anyone else as it was to me, consider Baez' two pinhole cameras, taking a picture when at the same place and time, but this time let's put the "plus sign" a little ahead of the camera that is tracking its motion, such that when the two cameras coincide, the stationary camera takes an image of the plus sign apparently at its point of closest approach. The plus sign is riding on a string through its horizontal piece, and the moving camera is trailing it on a parallel string that passes through the stationary camera.

So if the plus sign is moving left to right, this of course means the plus sign is really a bit to the right of the point of closest approach at the moment the cameras coincide and snap their photos. We know that the image from the stationary camera will show a length contracted horizontal piece, because we agree that there we can correctly reckon that it is length contracted. The moving camera, on the other hand, sees the plus sign as being a little rotated, because it is trailing it a bit, so the photo in the moving camera will also have a shortened horizontal piece. Baez is saying that the amount it will be shortened in this example is exactly the Lorentz factor, such that the shapes of the plus signs will be the same in the two photos. So to get the moving camera to coincide with the stationary one when the stationary one needs to snap this photo, the moving camera must trail the plus sign by exactly the angle needed to make the plus sign look Lorentz contracted. That the two images look the same is the basis for saying length contraction is "invisible"-- it's an ambiguity between whether the visible length contraction is real as for the stationary camera, or due to rotation as for the moving camera, when just looking at the "literal" images. This would seem to be a special feature of Lorentz contraction, perhaps an equivalent way to assert the postulates of relativity.

 

[JDoolin]

Light is not like bullets. If we are in flat space time and the rest frame of the camera is inertial, then light is propagating isotropically in all directions from each emission point in the rest frame of the camera, so the wave fronts reaching the static camera are perpendicular to the straight line between the camera and the emission point.

I would just change the word "point" to "event"

There is no aberration in the rest frame of the camera.

That is, there are no obliquely traveling wave-fronts of light from any event.

 

[JDoolin]

All right, thanks to everyone for clearing that up for me, I was definitely making aberration too difficult. My bad.

Anyway, I think I see that Baez is right, though Terrell's "invisibility" claim is still a bit of a stretch-- two cameras in relative motion that image the same object at the same place and time will always image the same shape, it will just appear to be in a different direction, and it can also have a different total angular size.

If how that could be is still as unclear to anyone else as it was to me, consider Baez' two pinhole cameras, taking a picture when at the same place and time, but this time let's put the "plus sign" a little ahead of the camera that is tracking its motion, such that when the two cameras coincide, the stationary camera takes an image of the plus sign apparently at its point of closest approach. The plus sign is riding on a string through its horizontal piece, and the moving camera is trailing it on a parallel string that passes through the stationary camera.

So if the plus sign is moving left to right, this of course means the plus sign is really a bit to the right of the point of closest approach at the moment the cameras coincide and snap their photos. We know that the image from the stationary camera will show a length contracted horizontal piece, because we agree that there we can correctly reckon that it is length contracted. The moving camera, on the other hand, sees the plus sign as being a little rotated, because it is trailing it a bit, so the photo in the moving camera will also have a shortened horizontal piece. Baez is saying that the amount it will be shortened in this example is exactly the Lorentz factor, such that the shapes of the plus signs will be the same in the two photos. So to get the moving camera to coincide with the stationary one when the stationary one needs to snap this photo, the moving camera must trail the plus sign by exactly the angle needed to make the plus sign look Lorentz contracted. That the two images look the same is the basis for saying length contraction is "invisible"-- it's an ambiguity between whether the visible length contraction is real as for the stationary camera, or due to rotation as for the moving camera, when just looking at the "literal" images. This would seem to be a special feature of Lorentz contraction, perhaps an equivalent way to assert the postulates of relativity.

Are you really coming back to the conclusion that you can't "see" Lorentz Contraction here? I hope I have helped you to understand aberration a bit better, but it was definitely not my goal to get you to come to that conclusion!

 

[m4r35n357]

I was previously going to point out a couple of no-cost programs that illustrate all the relevant effects (aberration/doppler/headlight); I now have the full information so here goes (search the web if you need to know more about what they do):
1. Real-time relativity. Windows/Mac downloads but runs under Wine in Linux. The author's SR primer is here.
2. A slower speed of light, Windows/Mac/Linux. Testbed for MIT's SR game framework, now starting to look like abandonware.
Enjoy!

 

[Ken G]

Are you really coming back to the conclusion that you can't "see" Lorentz Contraction here? I hope I have helped you to understand aberration a bit better, but it was definitely not my goal to get you to come to that conclusion!

No, I agree that the standard meaning of "see" is much broader than the limited meaning applied by Terrell. And I appreciate your efforts to elucidate all the various factors here!

What I'm actually saying is that it is the conclusion of Baez that appears to be correct, and I did not see that before. Baez' claim is that two cameras taking a picture at the same place and time will always photograph small shapes the same. The shapes may appear at different places in the visual field if one of the cameras is subject to aberration, and there can also be some changes in total angular size relating to similar issues, but the two shapes will be the same, i.e., a plus sign seen as having a given contrast in the lengths of its pieces in one photograph will have that same contrast in the other photograph as well, and that would not be true in Galilean relativity it seems. How to express that fact in words is a bit tricky!

 

[A.T.]

I was previously going to point out a couple of no-cost programs that illustrate all the relevant effects (aberration/doppler/headlight); I now have the full information so here goes (search the web if you need to know more about what they do):
1. Real-time relativity. Windows/Mac downloads but runs under Wine in Linux. The author's SR primer is here.
2. A slower speed of light, Windows/Mac/Linux. Testbed for MIT's SR game framework, now starting to look like abandonware.
Enjoy!

Here is another potential one:

http://www.visus.uni-stuttgart.de/u...vistic_Visualization_by_Local_Ray_Tracing.pdf

As future work, we plan to extend our software to a freely available tool usable for teaching in the context of Special Relativity. We want to allow the user to interactively explore relativistic effects by supporting import of arbitrary 3D models from common file formats and graphical interaction with the relevant visualization parameters, e.g., observer’s position, directions of motion, speed, and the different visual effects shown (geometric only, Doppler shift, and searchlight effect).

Maybe they have made it available already or would if enough people ask them. I think it would be a great tool.

 

[A.T.]

I would just change the word "point" to "event"

I said "point" because a meant a spatial point, not a point in space-time. Light is propagating isotropically in all directions of space, not of space-time.

 

[m4r35n357]

Maybe they have made it available already or would if enough people ask them. I think it would be a great tool.

I'd like to think so too but the paper is from 2010 and they don't even give the program a name to search for. At first glance at least some of the emphasis of their approach is on numerical "fudging" for efficiency. I think the approach taken by Real Time Relativity is "purer" mathematically. Section 10 of the primer deals with rendering via stereographic projection, and builds on the work of Penrose.
[UPDATE]
No sooner had I posted than I found a recent program by one of the authors called GeoVis here. Unfortunately it appears to be unavailable to the general public, and with a license that I can't be bothered to even read. Shame as apparently it's a Linux program, and that's one of my things . . .
[UPDATE 2] Try here.

 

[JDoolin]

I said "point" because a meant a spatial point, not a point in space-time. Light is propagating isotropically in all directions of space, not of space-time.

By point, did you mean a stationary point in the observer's reference frame, or a point attached to an object which may or may not be moving in the observer's reference frame?

Because I think we've pretty well established that if the light from a point (attached to an object) is isotropic in one reference frame, it is not isotropic if you moving fast with respect to that object. That's what the diagram in post 66 is showing, and what I tried to explain in more detail in the video in post 71 (How an isotropic arrangement of beams in one reference frame leads to a nonistropic arrangement of beams in another reference frame.)

Maybe I'm misunderstanding your meaning of the word isotropic here. In the diagram in post 66, you see that the intensity of the light must be much greater coming off the front side of the source than from the back end. But the speed of light is the same in all directions. So if by isotropic you mean "the same speed" I'd agree with you, but if by isotropic, you mean "the same intensity" I'd have to disagree with you.

 

[A.T.]

By point, did you mean a stationary point in the observer's reference frame

This.

 

[JDoolin]

Sorry about that. I have a tendency to compulsively edit my posts for a few minutes after posting. I may have added about three paragraphs since your response.

 

[A.T.]

I think the approach taken by Real Time Relativity is "purer" mathematically.

After reading this:
http://people.physics.anu.edu.au/~cms130/RTR/Physicist.html
"The 2D screen image is created using the computer graphics technique known as environment mapping, which renders the 3D virtual world onto a 2D cube map."

I'm not sure if this accounts for differential signal delays, which are key to the visual effects for close passing by objects discussed here. It depends how it "renders the 3D virtual world onto a 2D cube map". The 4D-raytracing approach seems to be the most general to me.

 

[A.T.]

So if by isotropic you mean "the same speed"

This.

 

[PAllen]

No, I agree that the standard meaning of "see" is much broader than the limited meaning applied by Terrell. And I appreciate your efforts to elucidate all the various factors here!

What I'm actually saying is that it is the conclusion of Baez that appears to be correct, and I did not see that before. Baez' claim is that two cameras taking a picture at the same place and time will always photograph small shapes the same. The shapes may appear at different places in the visual field if one of the cameras is subject to aberration, and there can also be some changes in total angular size relating to similar issues, but the two shapes will be the same, i.e., a plus sign seen as having a given contrast in the lengths of its pieces in one photograph will have that same contrast in the other photograph as well, and that would not be true in Galilean relativity it seems. How to express that fact in words is a bit tricky!

And I claim that is false and provable from my detailed analysis of the moving rod. If you had a cross (with equal arms in its rest frame) with one arm in the direction of motion, then there would be one moment where the length of one arm would be shorter by gamma than the other arm. A camera at rest with respect to the cross at the same time would not see this. This is actually in agreement with Terrell (but not Baez if you quote him correctly). Terrell would say that the moving cross looks rotated such that one arm does have shorter angular span than the other. My analysis agrees with rotation (as one possible visual interpretation) in that the markings on the shorter arm would be stretched on one side and compressed on the other in a way that precisely matches rotation. However, if you imagined this arm parallel to motion as hollow, moving along rigid rod at rest with respect to the camera, you would be forced to re-interpret the same image as contraction with stretching and compression, because rotation could no longer be sustained as a visual interpretation. Penrose actually makes this point in his book "Road to Reality" that the rotation interpretation would interfered with if you introduce other objects moving at different speeds (he mentioned a track rather than hollowed out arm I proposed).

[I used brute force ray tracing in my analysis with no prior assumptions. I posted the resulting formulas, but not the derivation. If I have time at some point, I may post the derivation (it is actually only a page long on my hand written sheet). ]

[Edit1: One caveat, is that I have not analyzed the image for the camera co-moving with the cross, located at the same place and time as the camera taking the image I described above. It is possible that such an analysis could vindicate Baez as follows: in the frame of this camera co-moving with the cross, the cross is not being viewed head on, but substantially displaced; that is, at rest but far from head on in the direction of one arm. Then that arm would subtend less angle, and show distortion consistent with rotation. If that is the case, then Baez is vindicated (in the sense that both cameras would see a distorted cross). Again, if I have time in the future I will try to check whether this is what occurs. At this moment, I am suspecting that it does, and Baez is right, but in a different sense than Ken G. implies above.]

[Edit2: Further, if I am right in how Baez is correct in a certain sense, the if you start from a camera at rest with respect to the cross looking head on, and ask about a camera passing by at high speed snapping at that moment, what it would see is a non-distorted cross shifted a good distance forward, such that the light delay induced stretching compensates for the length contraction. Thus, a big part of this is simply that what one camera sees as 'head on' the other [momentarily colocated camera] sees as displaced in such a way that the combination of effects (displacement, light delay, contraction) preserves the shape.

So, while this is all interesting, it remains true for watching the cross go by:

1) There will be a time when one of its arms is shorter by gamma (and, at this time, it will look like it is being viewed head on - equidistant on either side of your line of sight). It is really hard for me to accept any definition of 'seeing' that doesn't call this directly seeing length contraction (despite the somewhat perverse way Baez's claim may remain true, as outlined in edit1).

2) At all times, length contraction is visible in the obvious way that if you account for light delays without assuming length contraction, you predict the wrong image. Thus what you see is at all times directly seeing what is expected by length contraction, and not what you would see without it.

]

 

[JDoolin]

If you line the

I was previously going to point out a couple of no-cost programs that illustrate all the relevant effects (aberration/doppler/headlight); I now have the full information so here goes (search the web if you need to know more about what they do):
1. Real-time relativity. Windows/Mac downloads but runs under Wine in Linux. The author's SR primer is here.
2. A slower speed of light, Windows/Mac/Linux. Testbed for MIT's SR game framework, now starting to look like abandonware.
Enjoy!

I just now played a slower speed of light, on my machine... Although my graphics card is woefully insufficient for smooth graphics, I was able to get through the game at lowest resolution and some choppy graphics. I thought it was quite nice; artistically done, and enjoyable and probably a lot more fun on a gaming computer. There was a question I have related to the graphics though.

When I got up to 30, 40, 50 percent of the speed of light, I was happy to find, as I would expect, that when I accelerated toward objects, they immediiately receded into the background, and when I backed up, the objects sprang forward. That is totally what I would have expected from aberration.

However, I was trying hard to watch the cross-section of objects against the ground. While the ground in front of me, itself, stretched out significantly, the actual mushroom and hut cross-sections against the ground did not seem to be stretched. So I'm wondering if I'm actually seeing the phenomenon that Penrose, Terrell and/or Baez is talking about? Or did the programmers shortcut the rendering of the huts, and just render them as circular huts and circular mushrooms? If the demonstration represents an accurate rendering, I'll have to eat my words... But I can't imagine How could the ground appear stretched, while the objects along the ground do not appear stretched by the same ratio?

I couldn't see any aberration in the shapes of individual objects until the very end, when I collected the final watermelon. Then the aberration in the yz-plane (away and vertical) became plainly visible. However, I still don't think I saw aberration in the xy-plane. (away and horizontal.)

 

[Ken G]

And I claim that is false and provable from my detailed analysis of the moving rod. If you had a cross (with equal arms in its rest frame) with one arm in the direction of motion, then there would be one moment where the length of one arm would be shorter by gamma than the other arm.

Yes, I originally thought that had to make Baez wrong. But it's not something he would likely get wrong, so it's very odd. I agree that if you put the moving camera right across from the moving cross, it has to see a symmetric cross at all times. But it certainly doesn't seem like the stationary camera will see a symmetric cross when the two cameras coincide in that case (though I suggested a different case where it seems like they might both see a contracted horizontal arm), because in this case, the image at that moment won't look like it is at the point of closest approach, it will look like it hasn't gotten there yet. But that should still make it look asymmetric. So we seem to have a case where one image looks symmetric, and the other doesn't. But this is in stark contrast to the conclusion of both Terrell and Baez, who cite high-powered mathematics and seem to understand exactly what they are saying.
What Baez says is:
"First, circles go to circles under the pixel mapping, so a sphere will always photograph as a sphere. Second, shapes of objects are preserved in the infinitesimally small limit. "
This seems to also be said by Terrell:
" Observers photographing the meter stick simultaneously from the same position will obtain precisely the same picture, except for a change in scale given by the Doppler shift ratio, irrespective of their velocity relative to the meter stick."

Terrell would say that the moving cross looks rotated such that one arm does have shorter angular span than the other.

Terrell does at one point say it won't look contracted, it will look rotated, but a rotated cross does not look like "precisely the same picture".

My analysis agrees with rotation (as one possible visual interpretation) in that the markings on the shorter arm would be stretched on one side and compressed on the other in a way that precisely matches rotation.

I don't understand that, wouldn't rotation contract all the tickmarks on the horizontal arm? But more importantly, we cannot even compare different tickmark lengths, because both Terrell and Baez are talking about an effect that is first order in smallness (the "infinitesmally small limit"), so no second order terms like a gradient in the stretching.

However, if you imagined this arm parallel to motion as hollow, moving along rigid rod at rest with respect to the camera, you would be forced to re-interpret the same image as contraction with stretching and compression, because rotation could no longer be sustained as a visual interpretation. Penrose actually makes this point in his book "Road to Reality" that the rotation interpretation would interfered with if you introduce other objects moving at different speeds (he mentioned a track rather than hollowed out arm I proposed).

But note that does not say the stationary camera would not also see something it could interpret as a rotation, so this doesn't speak to the issue of differences between the images.

It is possible that such an analysis could vindicate Baez as follows: in the frame of this camera co-moving with the cross, the cross is not being viewed head on, but substantially displaced; that is, at rest but far from head on in the direction of one arm. Then that arm would subtend less angle, and show distortion consistent with rotation. If that is the case, then Baez is vindicated (in the sense that both cameras would see a distorted cross). Again, if I have time in the future I will try to check whether this is what occurs. At this moment, I am suspecting that it does, and Baez is right, but in a different sense than Ken G. implies above.]

Actually, the scenario you describe here is exactly the one I described above. (Ignore the false turn on aberration, you are right that aberration only appears for a camera we regard as moving.) I figured that's what made Baez right, but what about the case where the moving camera is directly across from the cross, where it will always see a symmetric cross-- how could the stationary camera see that when they coincide? It doesn't seem like the stationary camera would ever see that, but if it ever does, then Baez must be right. If not, then I'm confused about what they mean by preserving the "shape of an object"-- if I take a cross in my hand, and rotate it, is that the same shape only rotated, or a different shape?

 

[Ken G]

If the demonstration represents an accurate rendering, I'll have to eat my words... But I can't imagine How could the ground appear stretched, while the objects along the ground do not appear stretched by the same ratio?

Could it be the difference between first-order-small effects that don't show any difference, and larger-solid-angle pictures where you start to see the distortions? Terrell only ever claimed that small shapes appeared the same, larger images require some type of cobbling together that might involve bringing in "non-literal" information, analogous to how all local frames in GR are Minkowski but the equivalence principle breaks down on larger scales.

 

[PAllen]

I'll comment more later, for now, just this.

Terrell does at one point say it won't look contracted, it will look rotated, but a rotated cross does not look like "precisely the same picture". I don't understand that, wouldn't rotation contract all the tickmarks on the horizontal arm?

Not at all. One side gets closer to you, the other side further away. The angle subtended by markings closer to you will be greater than those further away. The result I got for this effect precisely matches rotation, so I find it very hard to believe this is not what Terrell is referring to. Penrose also describes this effect.

But more importantly, we cannot even compare different tickmark lengths, because both Terrell and Baez are talking about an effect that is first order in smallness (the "infinitesmally small limit"), so no second order terms like a gradient in the stretching.

I don't necessarily think their results are that limited. A small object can still have markings on it.

Actually, the scenario you describe here is exactly the one I described above. (Ignore the false turn on aberration, you are right that aberration only appears for a camera we regard as moving.) I figured that's what made Baez right, but what about the case where the moving camera is directly across from the cross, where it will always see a symmetric cross-- how could the stationary camera see that when they coincide? It doesn't seem like the stationary camera would ever see that, but if it ever does, then Baez must be right. If not, then I'm confused about what they mean by preserving the "shape of an object"-- if I take a cross in my hand, and rotate it, is that the same shape only rotated, or a different shape?

When what you call the stationary camera coincides and sees a symmetric cross, in that camera's frame its viewing is NOT head on at that event. Aberration will have change the incoming light angle such that the image appears to still be approaching, and the light delay stretching will compensate for the length contraction such that it produces a symmetric photograph.The one case I can't quite resolve is that a rapidly approaching cross still far away will have the parallel (to motion) arm greatly stretched by light delay (by much more than length contraction can compensate, when it is far away). I can't find an all stationary analog of this case.

[edit: I think I resolved this last case, so there no discrepancies between my understanding and Terrell (Baez?), except for describing any of this as not seeing length contraction.

The resolution for approach is to consider a camera stationary relative to the cross, but displaced, sees some subtended angle for the shorter arm as e.g. 3 degrees, with a viewing angle of, say 40 degrees to the left. Then, a moving camera approaching the cross, momentarily coinciding with this camera, sees the same 3 degree subtended angle, the viewing angle is interpreted as much more than 40 degrees off head on. Thus, compared to a similar cross stationary with respect this 'moving camera', at the same viewing angle, the moving cross will appear to have one arm very elongated.

Properly accounting for frame dependence of viewing angle appears to resolve all remaining anomalies, as I see it.]