Time Dilation & Length Contraction: Graphically Explained

[Tomas Vencl]

TL;DR Summary

Time dilation and length contraction graphically

The thread "twin paradox without math" inspired me try to find fully graphical solution of length contraction.
Here is the result:

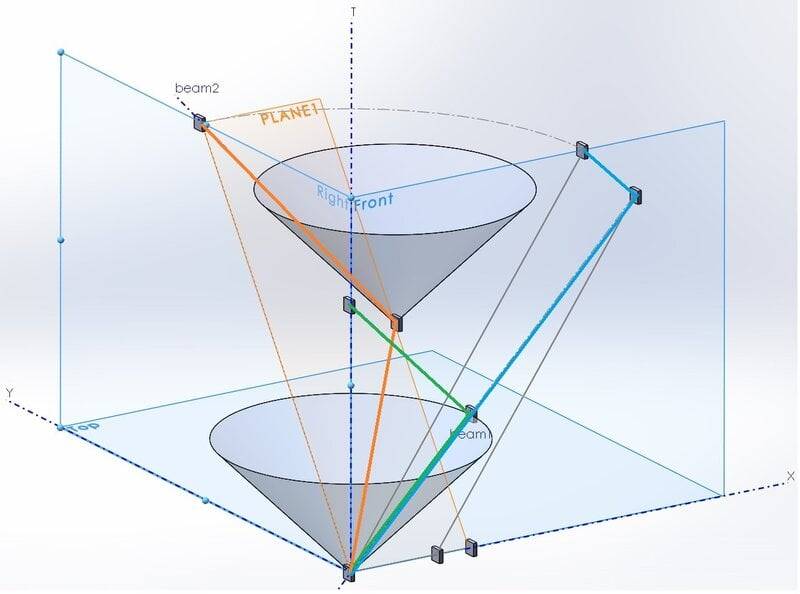
Graph is 3D as I think that is ilustrative to make all in one graph, but I am sure that it is possible to do it in 2 or 3 2D slices.
X and Y are spatial axes, T is time (static observer), light cone is 45 degree, so this is Minkowski spacetime.
There are 3 sets of light clocks at the picture.
The green one is standard static (in front plane) light clock (one tick) and defines scales of the axes (for example, if mirors are 1light second distant, the tick last 2 seconds).
The orange light beam is 2 second tick of moving (along Y axe, in plane 1) clock. The orange beam is intersection of plane 1 and lightcone surface.
The blue light beam is 2 second tick of clock moving along X axe. Because all clocks shoud show the same time independently on their orientation (at given speed), the 2 second tick of blue clocks should have the same duration as orange clocks. From this condition you can derive length contaction. Simply draw 45 degree blue lines from origin and final position of first mirror of blue clocks and their intersection defines necessary event of reflecting beam at second mirror of blue light clocks. This also define length contaction of blue light clocks.

 

[Orodruin]

Sorry to say, but I don’t think this diagram is clear at all. Particularly as you can easily make the graphical argument with two clocks only while only including a single spatial direction (the direction of motion).

 

[vanhees71]

Also one must note that you cannot interpret lengths in a Minkowski diagram in the Euclidean way, i.e., the unit marks on the axes of different inertial frames have not the same Eucldean but the same Minkowskian "length", i.e., they have to be constructed by the space- and time-like unit hyperbolae. I also think Minkowski diagrams are only helpful when discussing one-dimensional motions, i.e., when you have a time-space plane. Then the unit hyperbolae are given (for pseudo-Euclidean, i.e., Lorentzian coordinates)
$$(c t)^2-x^2=\pm 1.$$

 

[Tomas Vencl]

Also one must note that you cannot interpret lengths in a Minkowski diagram in the Euclidean way, i.e., the unit marks on the axes of different inertial frames have not the same Eucldean but the same Minkowskian "length", i.e., they have to be constructed by the space- and time-like unit hyperbolae. I also think Minkowski diagrams are only helpful when discussing one-dimensional motions, i.e., when you have a time-space plane. Then the unit hyperbolae are given (for pseudo-Euclidean, i.e., Lorentzian coordinates)
$$(c t)^2-x^2=\pm 1.$$

Yes, when you construct the "orange clocks tick" for different motions of orange clocks (different angle of plane 1), you receive this hyperbola (yellow, second positions of first orange miror for different orange clocks movements along Y axe).
Hyperbola is at Y-T plane, the other yellow line is only asymptote at 45 degree for easier orientation in graph.

 

[Tomas Vencl]

Maybe I should add some remarks. This is Minkowski spacetime, and axis X,Y,T are valid only for static observer.
The motion of orange clocks is one-dinesional, along Y axe, The motion of blue clocks i also one dimensional, along X axe.

 

[robphy]

I encourage you to continue making (2+1)-dimensional spacetime visualizations!
Sometimes they give insights that are not so easy to see in the (1+1)-case.

I think 3D-visualizations are more useful when a viewer can see multiple viewpoints
(possibly interactively, using say geogebra.org - see below)
as opposed to a static image... unless there are enough labels, formulae, or visual cues.

Your diagrams are nice.
Some suggestions:

• It might be good to draw the full "1 tick to the future" hyperboloid (asymptotic to the light cone of the origin event) on which the reception events lie.
• It also might be good to draw the past light cones of those reception events,
  and their intersections with the future light cone of the origin event.
  The intersections locate the hyperplanes of simultaneity of those clocks.
  You may also find that (2+1)-dimensional volumes enclosed by those cones are equal in magnitude (i.e. is a Lorentz variant quantity).
• If you also draw the transverse light clock moving along the forward X-axis,
  you would have drawn the spacetime diagram of the Michelson-Morley experiment (with Length Contraction).
• Possibly useful:
  Tevian Dray's "Using Three-dimensional Spacetime Diagrams in Special Relativity"
  https://ir.library.oregonstate.edu/downloads/5d86p0819
  American Journal of Physics 81, 593 (2013); https://doi.org/10.1119/1.4812591

Spoilers: here is my spacetime visualization of the Michelson Morley experiment.
https://www.geogebra.org/m/XFXzXGTq
which requires a (2+1)-dimensional spacetime diagram

Spolier: my visualization of a circular light clock (with references)
https://www.geogebra.org/m/pr63mk3j

In each, one can see time dilation and length contraction.

Spoilers: my (2+1)-dimensional spacetime visualizations (made with VPython)
my visualization suggesting the necessity of length contraction
VisualizingProperTime - Length Contraction
and
my visualization of the clock effect displaying the mechanism of a ticking light clock.
VisualizingProperTime - the Clock Effect / Twin Paradox with Circular Light Clocks (with audio)

(My comments from the other thread: https://www.physicsforums.com/threads/understanding-twin-paradox-without-math.1047245/post-6822789 )

 

[Tomas Vencl]

...

Thank you for your inspiring reply.