Tethebal| problem, radial acceleration, angle of ball orbit

[izforgoat]

Homework Statement

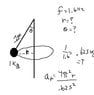
This is a concept/procedure question. I am playing teth3rbalI with a 1 kilogran ball and it is tied to a meterlong string. When I hit the ball it circles the pole at 1.6 Hz. Find the anglethat the string makes with thepole.

Homework Equations

a_{r}=v^{2}/r
a_{r}=(4\pi^{2}r)/T^{2}

T=1/f
f_{r}=ma_{r}

The Attempt at a Solution

So I found the period for one cycle but that's basically it and I'm stuck without a radius or at least a velocity to go by. What am I overlooking?

 

[Shooting Star]

The whirling string has to make an angle, say 'x', with the vertical in the downward direction. It lies on a cone, whose semi-vertical angle is 'x'. If 'T' is the tension in the string, then mg=T*cos(x). The centipetal force is T*sin(x). The mass m travels in a horizontal plane.

Now you try for a while.

 

[izforgoat]

hmmm

k so wow, i' not getting very far at all on this.

since Tcos(x) = mg then Tcos(x) = 9.8 N and since T sin(x) = centripedalforce then Tsin= 1kg((4\pi^{2}r)/(.625^{2}))

I'm slightly nervous proceeding since my next move would be to do a pythagoras of 9.8^{2} + ((4\pi^{2}r)/TimePeriod^{2})^{2} = T^{2} which doesn't seem right nor does it make me any more confident.

 

[izforgoat]

kk think i got it but does the mass cancel out?

 

[Shooting Star]

It'd be neater if you didn't write the values of g etc in every step. Use symbols and plug in the values later.

Yes, the mass cancels out.

The centripetal force is m*w^2*r= T*sin x.

tan x = Tsin x/Tcos x = mw^2*r/mg =rw^2/g.

You know the value of r, and w is given.

 

[cristo]

kk think i got it but does the mass cancel out?

If you look at Shooting Star's post this should become apparent.

It would also help if you formatted your posts in a more readable way. For example [ tex] [ /tex] tags should be used for LaTeX set on its own, whereas you should use [ itex] [ /itex] tags for inline maths. Furthermore, it would help if you either did all your equations in tex, or none of them, since that would prevent strange mixed formatting.

Just a few thoughts, anyway.