greypilgrim
- 581
- 44
Hi.
The angular resolution is calculated through
$$\theta=1.22\frac{\lambda}{D}\enspace.$$
It's the first zero of the intensity function (in small-angle approximation) of the Airy disk:
$$I\left(\alpha\right)=I_0\left(\frac{2J_1\left(\pi\cdot\alpha\cdot\frac{D}{\lambda}\right)}{\pi\cdot\alpha\cdot\frac{D}{\lambda}}\right)^2$$
So if the angle between two light sources is ##\theta##, the central maximum of one source coincides with the first minimum of the other and vice versa.
Though this makes sense, I tried a different approach and tried to find the smallest ##\theta## where the central peak of
$$I\left(\alpha\right)+I\left(\alpha-\theta\right)$$
divides into two. This happens way earlier, at about ##\theta\approx0.94\frac{\lambda}{D}##:
##\theta=0.90\frac{\lambda}{D}:##
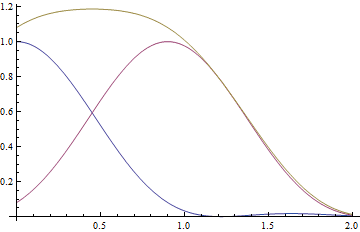
##\theta=0.94\frac{\lambda}{D}:##
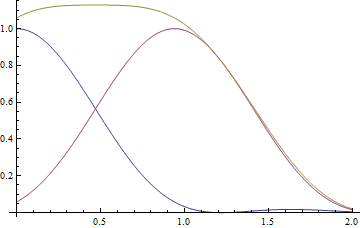
##\theta=1.00\frac{\lambda}{D}:##
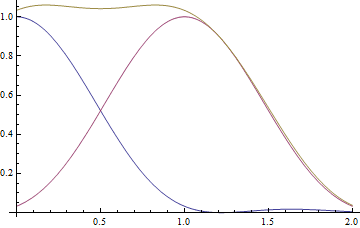
Wouldn't it make more sense to define ##\theta\approx0.94\frac{\lambda}{D}## as angular resolution?
The angular resolution is calculated through
$$\theta=1.22\frac{\lambda}{D}\enspace.$$
It's the first zero of the intensity function (in small-angle approximation) of the Airy disk:
$$I\left(\alpha\right)=I_0\left(\frac{2J_1\left(\pi\cdot\alpha\cdot\frac{D}{\lambda}\right)}{\pi\cdot\alpha\cdot\frac{D}{\lambda}}\right)^2$$
So if the angle between two light sources is ##\theta##, the central maximum of one source coincides with the first minimum of the other and vice versa.
Though this makes sense, I tried a different approach and tried to find the smallest ##\theta## where the central peak of
$$I\left(\alpha\right)+I\left(\alpha-\theta\right)$$
divides into two. This happens way earlier, at about ##\theta\approx0.94\frac{\lambda}{D}##:
##\theta=0.90\frac{\lambda}{D}:##
##\theta=0.94\frac{\lambda}{D}:##
##\theta=1.00\frac{\lambda}{D}:##
Wouldn't it make more sense to define ##\theta\approx0.94\frac{\lambda}{D}## as angular resolution?


