The force of magnitude F acts along the edge of the triangular plate

Click For Summary

Discussion Overview

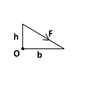
The discussion revolves around determining the moment of a force acting along the edge of a triangular plate about a specified point O. Participants explore various methods for calculating the moment, including the use of vector cross products and the implications of different coordinate representations.

Discussion Character

  • Homework-related, Technical explanation, Debate/contested

Main Points Raised

  • Some participants express confusion about how to apply the moment equation M = r x F, particularly in defining the position vector r and the force vector F.
  • One participant suggests using the top left point of the triangle as the reference point for the position vector, leading to a discussion about the components of the force vector.
  • Another participant proposes that the moment can be calculated as Fbh/(h^2+b^2)^(0.5), but acknowledges that answers may vary based on the method used.
  • There is a discussion about the components of the force vector, with one participant indicating that the y-direction is significant for calculating the moment, while the x-direction does not contribute.
  • Some participants discuss the implications of the cross product and how to handle the components of the vectors involved, raising questions about the distribution property in vector cross products.
  • One participant questions whether the position vector can be defined from any point along the line of action of the force, leading to clarification about the starting point of the position vector.
  • A later reply emphasizes the importance of not doing the student's homework for them, suggesting that guidance should focus on hints and corrections rather than providing complete solutions.

Areas of Agreement / Disagreement

Participants generally express confusion and uncertainty about the calculations involved, with no clear consensus on the correct approach or final answer. Multiple competing views on how to define vectors and calculate moments remain unresolved.

Contextual Notes

Limitations in the discussion include varying interpretations of the position vector and force vector, as well as the potential for different methods to yield different results. Some participants express difficulty in articulating their mathematical reasoning without proper notation.

pyroknife
Messages
611
Reaction score
4

Homework Statement


I attached the drawing.
The force of magnitude F acts along the edge of the triangular plate. Determine the moment of F about point O.

Homework Equations



M=rxF

The Attempt at a Solution


What I did was I just picked the top left point of the triangle and labeled that (0,h) which give me my r vector 0i+hj. After that I really don't know how to proceed except to find the angle by doing inverse tangent of h/b, but I just keep getting variable after variable. What other way is there to do this?
 

Attachments

  • Untitled.png
    Untitled.png
    3.5 KB · Views: 1,547
Physics news on Phys.org


pyroknife said:

Homework Statement


I attached the drawing.
The force of magnitude F acts along the edge of the triangular plate. Determine the moment of F about point O.

Homework Equations



M=rxF

The Attempt at a Solution


What I did was I just picked the top left point of the triangle and labeled that (0,h) which give me my r vector 0i+hj. After that I really don't know how to proceed except to find the angle by doing inverse tangent of h/b, but I just keep getting variable after variable. What other way is there to do this?

F is

b i - h j

what matters is the y direction for it is perpendicular and x is forming no moment

you just (bi) cross (-hj) to get ( -bh ) k, a vector of bh magnitude into the page.
 


The answer is supposed to be Fbh/(h^2+b^2)^.5. Answers do vary tho according to method, but I don't think yours matches this
 


pyroknife said:
The answer is supposed to be Fbh/(h^2+b^2)^.5. Answers do vary tho according to method, but I don't think yours matches this

YES sorry I made a very Fundamental mistake and will try to rectify it


F= F *( b / ( h**2+b**2 ) ** 0.5 ) i + F*( h / ( h**2+b**2 ) ** 0.5 ) j

Fx * h = is the answer F*b*h *(h**2+b**2 ) ** -0.5

which is into the page
 


I'm still a little confused. I would like to do all moment problems by using M=rxF. How would that work in this problem. i can get the F vector but it's going to look really messy because I got to define the angle theta as tangent inverse of (b/h) then take the cosine of the tangent inverse of (b/h) to get the x component and same for the y.
 


pyroknife said:
I'm still a little confused. I would like to do all moment problems by using M=rxF. How would that work in this problem. i can get the F vector but it's going to look really messy because I got to define the angle theta as tangent inverse of (b/h) then take the cosine of the tangent inverse of (b/h) to get the x component and same for the y.


M=r X F is already defined to be M= ( rx i + ry j + rz k ) X ( Fx i + Fy j + Fz k )

here simply r X ( Fx i + Fy j ) = r X Fx i + rXFy j by distribution property

but here : r= h j what do you get when you cross j by j ? for the latter part, of course a zero

here rXFyj drops and we are left with r X Fx i , here you cross jXi which points in the direction into the page.
 


stallionx said:
M=r X F is already defined to be M= ( rx i + ry j + rz k ) X ( Fx i + Fy j + Fz k )

here simply r X ( Fx i + Fy j ) = r X Fx i + rXFy j by distribution property

but here : r= h j what do you get when you cross j by j ? for the latter part, of course a zero

here rXFyj drops and we are left with r X Fx i , here you cross jXi which points in the direction into the page.

its so hard to write all this online w/o subscripts and stuff. can r=b i too?
 


pyroknife said:
its so hard to write all this online w/o subscripts and stuff. can r=b i too?

Sir,

r is starting from ( 0, 0 ) ---> take origin

and

draw a vector to the APPlication point of F.

r begins at ( 0,0 ) ends at application point of F.
 


stallionx said:
Sir,

r is starting from ( 0, 0 ) ---> take origin

and

draw a vector to the APPlication point of F.

r begins at ( 0,0 ) ends at application point of F.

what I asked was basically the ending point can be any point on the line of action right?
 
  • #10


pyroknife said:
what I asked was basically the ending point can be any point on the line of action right?

No Sir, position vector starts at wherever you take the moment ( here (0,0) ) with respect to, and ends at starting point of F. ( which is h units above the (0,0)
 
  • #11


stallionx said:
YES sorry I made a very Fundamental mistake and will try to rectify it


F= F *( b / ( h**2+b**2 ) ** 0.5 ) i + F*( h / ( h**2+b**2 ) ** 0.5 ) j

Fx * h = is the answer F*b*h *(h**2+b**2 ) ** -0.5

which is into the page

You need to stop doing the student's homework for them. You may provide hints, ask questions, find mistakes, etc. But it is against the PF rules to do the student's work for them.
 

Similar threads

Another moment question, completely lost
  • · Replies 4 ·
Replies
4
Views
3K
How Do I Find the Tension in the Cable AB Given Forces and Angles?
  • · Replies 1 ·
Replies
1
Views
3K
Find the force acting on the roller in the direction of the spring
  • · Replies 14 ·
Replies
14
Views
2K
Resultant force and its point of action
  • · Replies 9 ·
Replies
9
Views
3K
Finding an unknown force at an unknown angle
  • · Replies 9 ·
Replies
9
Views
5K
Why is this force considered in the moment equation?
  • · Replies 4 ·
Replies
4
Views
2K
Force acting on a dielectric placed between parallel plates
  • · Replies 5 ·
Replies
5
Views
2K
Analyzing the Mechanics of a Wobble Plate in a Cranked Axle Mechanism
  • · Replies 10 ·
Replies
10
Views
4K
Find Magnitude of F to Cause Net Effect of 3 Forces: Stress in Bolt
  • · Replies 4 ·
Replies
4
Views
5K
Resolve force into components along different paths
  • · Replies 5 ·
Replies
5
Views
13K