Korisnik
- 62
- 1
I'm stuck on some high school physics, Gauss law...
1. It says this: The electric field outside the sphere is equal as if the charge of the sphere was in it's center.
I don't understand this, why is this true? I get it - experiments have showed that and that's how you calculate it; but what's the reasoning behind it?
My explanation: Is it the same as if for example we had 2 different (in size) charges of opposite signs that are at a small distance from each other. Then when we are closer to the smaller one, let's say a negative one, we feel the negative force (if that was possible), but as we move away from it, we feel the positive force of the other charge (which is positive and more "charged"). So when we are a mile away from both these charges, we actually feel only the positive force, and don't even know there is actually a smaller negative charge next to the positive one. I think it has something to do with that, but I can't understand it completely.
2. It says this: If we imagine 2 cylinders with the same base of area S on a charged board (Q charged). The "force lines" that are coming out of that part of the board are going through the two second bases of the cylinders so the strength of the electric field by Gauss law:
\begin{equation}E=\frac{Q}{2\epsilon S}.\end{equation}
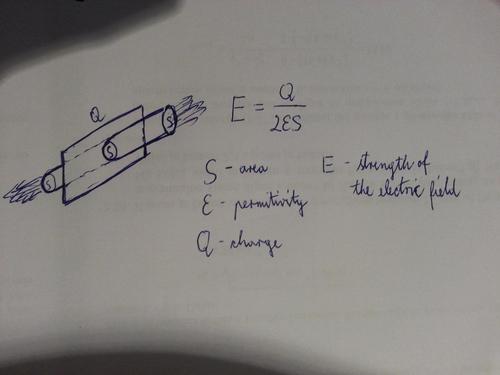
Sorry because of the bad drawing, the cylinders are attached to the board in 90°...
I'm not quite sure what they mean by this text... Do they mean - because the force lines are only going in these directions on a charged plate (←→), if you connect a non-conducting (? they don't say what kind of a cylinder it is) cylinder, they would still go in these directions, because of the polarisation of the cylinder. If it doesn't polarize, if it's a conductor - then both of the charges will flow in any of the directions (depending on the fact in which cylinder they flew into), and they will accumulate on the flat surface, while not many will accumulate on the curved one (?)...
Thanks for help in advance.
1. It says this: The electric field outside the sphere is equal as if the charge of the sphere was in it's center.
I don't understand this, why is this true? I get it - experiments have showed that and that's how you calculate it; but what's the reasoning behind it?
My explanation: Is it the same as if for example we had 2 different (in size) charges of opposite signs that are at a small distance from each other. Then when we are closer to the smaller one, let's say a negative one, we feel the negative force (if that was possible), but as we move away from it, we feel the positive force of the other charge (which is positive and more "charged"). So when we are a mile away from both these charges, we actually feel only the positive force, and don't even know there is actually a smaller negative charge next to the positive one. I think it has something to do with that, but I can't understand it completely.
2. It says this: If we imagine 2 cylinders with the same base of area S on a charged board (Q charged). The "force lines" that are coming out of that part of the board are going through the two second bases of the cylinders so the strength of the electric field by Gauss law:
\begin{equation}E=\frac{Q}{2\epsilon S}.\end{equation}
Sorry because of the bad drawing, the cylinders are attached to the board in 90°...
I'm not quite sure what they mean by this text... Do they mean - because the force lines are only going in these directions on a charged plate (←→), if you connect a non-conducting (? they don't say what kind of a cylinder it is) cylinder, they would still go in these directions, because of the polarisation of the cylinder. If it doesn't polarize, if it's a conductor - then both of the charges will flow in any of the directions (depending on the fact in which cylinder they flew into), and they will accumulate on the flat surface, while not many will accumulate on the curved one (?)...
Thanks for help in advance.