Fatima Hasan
- 315
- 14
Homework Statement
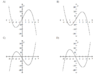
How to determine the graph using the properties of a twice-differentiable function ?
Homework Equations
None
The Attempt at a Solution
when x < 2 , y ' > 0 . So, the function is increasing on this interval. But , the correct answer is ( D) and the function is decreasing when x < 2.
Could somebody help me to solve this problem ?
Thank you for your help