The Mysterious Stabilization of a Spinning Top

  • Thread starter Thread starter aaaa202
  • Start date Start date
  • Tags Tags
    Spinning
AI Thread Summary
Spinning tops can stabilize due to the conservation of angular momentum, which allows them to maintain their upright position even after being struck. The phenomenon of precession plays a crucial role in this stabilization process. When a spinning top is disturbed, it can return to an upright position, suggesting that the interaction between the top's angular momentum and the surface affects its stability. The discussion hints at the importance of considering the contact point's imperfections in understanding this behavior. Overall, the mechanics behind a spinning top's stabilization involve complex interactions of forces and angular momentum.
aaaa202
Messages
1,144
Reaction score
2
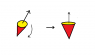
Everyone has seen a spinning top in action, and maybe some of you have also seen how they're able to stabilize completely like shown in the attached picture. I do get that they're hard to stop spinning because of conservation of angular momentum, but that they should be able to stabilize just seems weird.
 

Attachments

  • Unavngivet.png
    Unavngivet.png
    2.4 KB · Views: 480
Physics news on Phys.org
I think you misunderstood me. I'm asking how it's able to get back into the position where it stands completely upright after it's been struck and started to preces at angle. I am pretty sure I have seen that happen.
 
My immediate guess is that it might be useful to consider the consequences of the contact point not being a perfect mathematical point, and the resulting interaction between the angular momenta of the top and the surface on which it spins...
 
Thread 'Gauss' law seems to imply instantaneous electric field propagation'

Thread 'Gauss' law seems to imply instantaneous electric field propagation'

Imagine a charged sphere at the origin connected through an open switch to a vertical grounded wire. We wish to find an expression for the horizontal component of the electric field at a distance ##\mathbf{r}## from the sphere as it discharges. By using the Lorenz gauge condition: $$\nabla \cdot \mathbf{A} + \frac{1}{c^2}\frac{\partial \phi}{\partial t}=0\tag{1}$$ we find the following retarded solutions to the Maxwell equations If we assume that...
View full post »

Thread 'Do electron density waves accompany EM waves in coaxial cables?'

Maxwell’s equations imply the following wave equation for the electric field $$\nabla^2\mathbf{E}-\frac{1}{c^2}\frac{\partial^2\mathbf{E}}{\partial t^2} = \frac{1}{\varepsilon_0}\nabla\rho+\mu_0\frac{\partial\mathbf J}{\partial t}.\tag{1}$$ I wonder if eqn.##(1)## can be split into the following transverse part $$\nabla^2\mathbf{E}_T-\frac{1}{c^2}\frac{\partial^2\mathbf{E}_T}{\partial t^2} = \mu_0\frac{\partial\mathbf{J}_T}{\partial t}\tag{2}$$ and longitudinal part...
View full post »
Thread 'Recovering Hamilton's Equations from Poisson brackets'

Thread 'Recovering Hamilton's Equations from Poisson brackets'

The issue : Let me start by copying and pasting the relevant passage from the text, thanks to modern day methods of computing. The trouble is, in equation (4.79), it completely ignores the partial derivative of ##q_i## with respect to time, i.e. it puts ##\partial q_i/\partial t=0##. But ##q_i## is a dynamical variable of ##t##, or ##q_i(t)##. In the derivation of Hamilton's equations from the Hamiltonian, viz. ##H = p_i \dot q_i-L##, nowhere did we assume that ##\partial q_i/\partial...
View full post »

Similar threads

I Gyroscopic precession of a spin-stabilized bullet
Replies
10
Views
4K
I A scientific analysis of stopping the spin of Discovery One spaceship
Replies
3
Views
2K
I Rotating plate thrown parallel to ground
Replies
2
Views
1K
Why Does a Spinning Top Stabilize After Wobbling?
Replies
4
Views
9K
A Spinning a Slinky: Momentum & Angular Momentum Explained
Replies
22
Views
3K
A How to show spin ##= \pm 2/\omega## for a circ-polarized gravity wave
Replies
0
Views
1K
I Question about Stern-Gerlach experiment
Replies
12
Views
3K
I Angular momentum and turning a bicycle
Replies
17
Views
4K
I An ID-card sliding on a low friction table
Replies
14
Views
1K
Consider the hypothetical decay of the Φ(1020) meson into 3 pions
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top