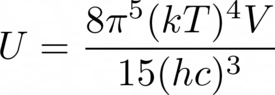SUMMARY
The discussion focuses on the pressure-entropy relationship for a photon gas as derived from the internal energy equation \( U = \sigma T^4 V \). The key conclusion is that the pressure \( P \) can be expressed as \( P = -\left(\frac{\partial U}{\partial V}\right)_S = \frac{U}{3V} \). It is established that when calculating the partial derivative, both entropy \( S \) and photon number \( N \) must be kept constant, while temperature \( T \) varies. The relationship is further supported by integrating the derived expressions and applying Nernst's Law.
PREREQUISITES
- Understanding of the first law of thermodynamics
- Familiarity with partial derivatives in thermodynamic contexts
- Knowledge of photon gas properties and behavior
- Basic principles of kinetic theory
NEXT STEPS
- Study the derivation of thermodynamic potentials for photon gases
- Learn about the implications of Nernst's Law in thermodynamics
- Explore the relationship between entropy and temperature in statistical mechanics
- Investigate the concept of chemical potential in non-conserved systems
USEFUL FOR
Students and professionals in physics, particularly those focusing on thermodynamics, statistical mechanics, and photon gas behavior. This discussion is beneficial for anyone looking to deepen their understanding of the pressure-entropy relationship in thermodynamic systems.