Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...
I am currently reading Chapter 5: The Riemann Integral and am currently focused on Section 5.1 Riemann Sums ... ...
I need some help in understanding the proof of Theorem 5.10 ...Theorem 5.10 and its proof read as follows:View attachment 9473
View attachment 9474
At the start of the above proof by Browder we read the following:
" ... ... The necessity of the condition is immediate from the definition of the integral ... ... "Can someone please help me to rigorously demonstrate the necessity of the condition ...
-------------------------------------------------------------------------------------------------------------------
Note: I am assuming that proving "the necessity of the condition is proving the following:$$\int_a^b f \text{ exists } \Longrightarrow$$ ... for every $$\epsilon \gt 0 \ \exists \ $$ a partition $$\pi$$ of $$[a, b]$$ such that $$\overline{S} (f, \pi) - \underline{S} (f, \pi) \lt \epsilon$$ ... ...
-------------------------------------------------------------------------------------------------------------------
Help will be much appreciated ...
Peter
==========================================================================================Note: It may help MHB readers of the above post to have access to Browder's notation, definitions and theorems on Riemann integration preliminary to Theorem 5.10 ... hence i am providing access to the same ... as follows:
View attachment 9475
View attachment 9476
View attachment 9477
View attachment 9478
Hope that helps ...
Peter
I am currently reading Chapter 5: The Riemann Integral and am currently focused on Section 5.1 Riemann Sums ... ...
I need some help in understanding the proof of Theorem 5.10 ...Theorem 5.10 and its proof read as follows:View attachment 9473
View attachment 9474
At the start of the above proof by Browder we read the following:
" ... ... The necessity of the condition is immediate from the definition of the integral ... ... "Can someone please help me to rigorously demonstrate the necessity of the condition ...
-------------------------------------------------------------------------------------------------------------------
Note: I am assuming that proving "the necessity of the condition is proving the following:$$\int_a^b f \text{ exists } \Longrightarrow$$ ... for every $$\epsilon \gt 0 \ \exists \ $$ a partition $$\pi$$ of $$[a, b]$$ such that $$\overline{S} (f, \pi) - \underline{S} (f, \pi) \lt \epsilon$$ ... ...
-------------------------------------------------------------------------------------------------------------------
Help will be much appreciated ...
Peter
==========================================================================================Note: It may help MHB readers of the above post to have access to Browder's notation, definitions and theorems on Riemann integration preliminary to Theorem 5.10 ... hence i am providing access to the same ... as follows:
View attachment 9475
View attachment 9476
View attachment 9477
View attachment 9478
Hope that helps ...
Peter
Attachments
-
 Browder - 1 - Theorem 5.10 ... PART 1 ... .png22.9 KB · Views: 145
Browder - 1 - Theorem 5.10 ... PART 1 ... .png22.9 KB · Views: 145 -
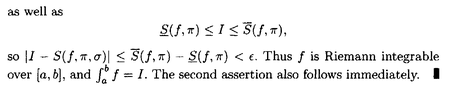 Browder - 2 - Theorem 5.10 ... PART 2 ... .png4.8 KB · Views: 148
Browder - 2 - Theorem 5.10 ... PART 2 ... .png4.8 KB · Views: 148 -
 Browder - 1 - Start of 5.1 - Relevant Defns & Propns ... PART 1 ... .png18.1 KB · Views: 147
Browder - 1 - Start of 5.1 - Relevant Defns & Propns ... PART 1 ... .png18.1 KB · Views: 147 -
 Browder - 2 - Start of 5.1 - Relevant Defns & Propns ... PART 2 ... .png57.5 KB · Views: 157
Browder - 2 - Start of 5.1 - Relevant Defns & Propns ... PART 2 ... .png57.5 KB · Views: 157 -
 Browder - 3 - Start of 5.1 - Relevant Defns & Propns ... PART 3 ... .png44.6 KB · Views: 147
Browder - 3 - Start of 5.1 - Relevant Defns & Propns ... PART 3 ... .png44.6 KB · Views: 147 -
 Browder - 4 - Start of 5.1 - Relevant Defns & Propns ... PART 4 ... .png43.2 KB · Views: 142
Browder - 4 - Start of 5.1 - Relevant Defns & Propns ... PART 4 ... .png43.2 KB · Views: 142
Last edited: