The Riemann and Darboux Integrals .... Browder, Theorem 5.10 .... ....

[Math Amateur]

TL;DR

I need help to prove a theorem effectively equivalencing Riemann and Darboux integration ...

I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...

I am currently reading Chapter 5: The Riemann Integral and am currently focused on Section 5.1 Riemann Sums ... ...

I need some help in understanding the proof of Theorem 5.10 ...Theorem 5.10 and its proof read as follows:

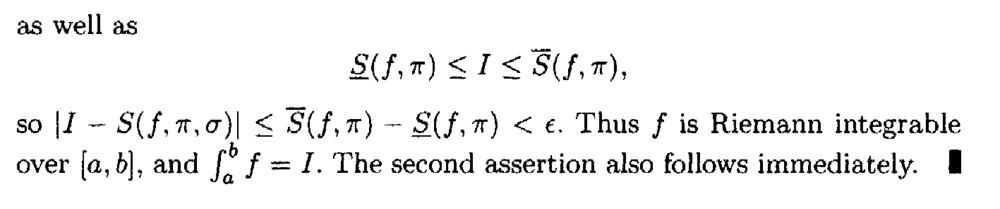
At the start of the above proof by Browder we read the following:

" ... ... The necessity of the condition is immediate from the definition of the integral ... ... " Can someone please help me to rigorously demonstrate the necessity of the condition ...

-------------------------------------------------------------------------------------------------------------------

Note: I am assuming that proving "the necessity of the condition is proving the following:$\int_a^b f \text{ exists } \Longrightarrow$ ... for every $\epsilon \gt 0 \ \exists \$ a partition $\pi$ of $[a, b]$ such that $\overline{S} (f, \pi) - \underline{S} (f, \pi) \lt \epsilon$ ... ...

-------------------------------------------------------------------------------------------------------------------

Help will be much appreciated ...

Peter
==========================================================================================Note: It may help Physics Forum readers of the above post to have access to Browder's notation, definitions and theorems on Riemann integration preliminary to Theorem 5.10 ... hence I am providing access to the same ... as follows:

Hope that text helps ...

Peter

 

[member 587159]

This would be a lot more readable if you just typed out the relevant definitions instead of a lot of images. That being said, here is how you can proceed (possibly I overcomplicated the matter though).

Let $\epsilon > 0$. Choose $\pi$ as in the definition of integral such that for all corresponding $\sigma$ we have $|S(f, \pi, \sigma)-I| < \epsilon/4$.

Since $\overline{S}(f, \pi) = \sup\{S(f, \pi, \sigma): \sigma \mathrm{\ associated \ to \ \pi}\}$, we can select $\sigma_1$ such that $\overline{S}(f, \pi)- S(f, \pi, \sigma_1)< \epsilon/4$. Similarly, one can choose $\sigma_2$ such that $S(f, \pi, \sigma_2) - \underline{S}(f, \pi) < \epsilon/4$

Then $\overline{S}(f, \pi) - \underline{S}(f, \pi) \leq |\overline{S}(f, \pi) - S(f,\pi, \sigma_1)| + |S(f, \pi, \sigma_1)-I| + |I-{S}(f, \pi, \sigma_2)|+ |S(f, \pi, \sigma_2)- \underline{S}(f, \pi, \sigma_2)| < \epsilon$

which is exactly what we want.

 

[fresh_42]

Hi Peter,

a good strategy is always to write down what we have. Here we have that $I:=\int_a^b f(x)\,dx$ exists. Therefore we have to look at definition 5.4. which tells us $|S(f,\pi,\sigma)-I|<\varepsilon_1\,$. Now we want to show that $|\underline{S}(f,\pi)-\overline{S}(f,\pi)|<\varepsilon_2\,$.

Whenever we see something like $|A-B|<\varepsilon$ then then triangle inequality lurks around the corner.
A standard procedure is now $|A-B|=|A-C + (C-B)| \leq |A-C|+|B-C|$ and the approximation of the two resulting summands to get an estimation of the original term.

 

[Math Amateur]

Thanks to fresh_42 and Math_QED for the hints ...

Based on your advice my proof proceeds as follows ...

We wish to prove:

$\int_a^b f \text{ exists } \Longrightarrow$] ... for every $\epsilon \gt 0 \ \exists \$ a partition $\pi$ of $[a, b]$ such that $\overline{S} (f, \pi) - \underline{S} (f, \pi) \lt \epsilon$ ... ...Proof:

Let $\int_a^b f = I$

Then

$I$ exists $\Longrightarrow$ for any $\frac{ \epsilon }{2} \gt 0 \ \exists \ \pi_0$ such that for any $\pi \geq \pi_0$ and every selection $\sigma$ associated with $\pi$ we have $| s(f, \pi, \sigma ) - I | \lt \frac{ \epsilon }{2}$Now $| S(f, \pi, \sigma ) - I | \lt \frac{ \epsilon }{2}$

implies that

$- \frac{ \epsilon }{2} \lt S(f, \pi, \sigma ) - I \lt \frac{ \epsilon }{2}$

and so, obviously, we have that

$S(f, \pi, \sigma ) - I \lt \frac{ \epsilon }{2}$ ... ... ... ... ... (1)But $| S(f, \pi, \sigma ) - I | \lt \frac{ \epsilon }{2}$

... also implies that

$- \frac{ \epsilon }{2} \lt I - S(f, \pi, \sigma ) \lt \frac{ \epsilon }{2}$

so, obviously, we have that

$I - S(f, \pi, \sigma ) \lt \frac{ \epsilon }{2}$ ... ... ... ... ... (2)

Now we also have that

$\underline{S} (f, \pi) \leq S(f, \pi, \sigma ) \leq \overline{S} (f, \pi)$ ... ... ... ... ... (3)Now (1) and (3) imply

$\overline{S} (f, \pi) - I \lt \frac{ \epsilon }{2}$ ... ... ... ... ... (4)Similarly (2) and (3) imply

$I - \underline{S} (f, \pi) \lt \frac{ \epsilon }{2}$ ... ... ... ... ... (5)Adding (4) and (5) gives

$\overline{S} (f, \pi) - \underline{S} (f, \pi) \lt \epsilon$ ... ...
Is that basically correct?

Peter

 

[member 587159]

Thanks to fresh_42 and Math_QED for the hints ...

Based on your advice my proof proceeds as follows ...

We wish to prove:

$\int_a^b f \text{ exists } \Longrightarrow$] ... for every $\epsilon \gt 0 \ \exists \$ a partition $\pi$ of $[a, b]$ such that $\overline{S} (f, \pi) - \underline{S} (f, \pi) \lt \epsilon$ ... ...Proof:

Let $\int_a^b f = I$

Then

$I$ exists $\Longrightarrow$ for any $\frac{ \epsilon }{2} \gt 0 \ \exists \ \pi_0$ such that for any $\pi \geq \pi_0$ and every selection $\sigma$ associated with $\pi$ we have $| s(f, \pi, \sigma ) - I | \lt \frac{ \epsilon }{2}$Now $| S(f, \pi, \sigma ) - I | \lt \frac{ \epsilon }{2}$

implies that

$- \frac{ \epsilon }{2} \lt S(f, \pi, \sigma ) - I \lt \frac{ \epsilon }{2}$

and so, obviously, we have that

$S(f, \pi, \sigma ) - I \lt \frac{ \epsilon }{2}$ ... ... ... ... ... (1)But $| S(f, \pi, \sigma ) - I | \lt \frac{ \epsilon }{2}$

... also implies that

$- \frac{ \epsilon }{2} \lt I - S(f, \pi, \sigma ) \lt \frac{ \epsilon }{2}$

so, obviously, we have that

$I - S(f, \pi, \sigma ) \lt \frac{ \epsilon }{2}$ ... ... ... ... ... (2)

Now we also have that

$\underline{S} (f, \pi) \leq S(f, \pi, \sigma ) \leq \overline{S} (f, \pi)$ ... ... ... ... ... (3)Now (1) and (3) imply

$\overline{S} (f, \pi) - I \lt \frac{ \epsilon }{2}$ ... ... ... ... ... (4)Similarly (2) and (3) imply

$I - \underline{S} (f, \pi) \lt \frac{ \epsilon }{2}$ ... ... ... ... ... (5)Adding (4) and (5) gives

$\overline{S} (f, \pi) - \underline{S} (f, \pi) \lt \epsilon$ ... ...
Is that basically correct?

Peter

How do (1) and (3) imply (4)?

Similarly for (2) and (3) implies (5).

 

[Math Amateur]

Hi Math_QED ...

Hmmm ... problem ... just checked ... the implications do not follow ... don't know what I was thinking ... apologies ..

Thanks again for your help ..

Peter

 

[member 587159]

Hi Math_QED ...

Hmmm ... problem ... just checked ... the implications do not follow ... don't know what I was thinking ... apologies ..

Thanks again for your help ..

Peter

No problem. A possible proof is in post #2.