Thermodynamic heating air problem

[Tusike]

Homework Statement

Hi! I apologize in advance for my knowledge of vocabulary in this topic:)

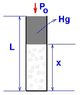
OK, so we have a Melde-tube 55 cm long, T=293K, with the top of it open, and a 20cm Hg part cutting off 30cm of air when is equilibrium. The original problem asked how much we can heat the air so that no Hg would come out of the tube, that's fairly easy.

My question is, what happens if we heat the air beyond that temperature? Because sure, we increased the temperature, but the Hg came out, and so the pressure decreased! I'm interested in some sort of V-T diagram beyond this point, or how to calculate the work done by the air after all the Hg came out of the tube.

Homework Equations

pV=nRT=NkT
dE = Q + W

The Attempt at a Solution

I really don't have much idea but I'll post the solution to the original problem so it'd be easier to calculate from beyond that point:

Gay Lussac 1: V1 / T1 = V2 / T2 -> L1 / T1 = L2 / T2

where L1 = 30cm, T1 = 293K, L2 = Lmax = 35 cm, T2 = ? = 35 / 30 * 293 = 342K.

Thanks for any help!

 

[hikaru1221]

I guess your Melde tube looks like something in the picture? Assume so, then this problem is quite interesting Let T1, P1, x1 denote the initial temperature, pressure and height of the air column (by "initial", I mean at the time Hg is raised to the top).

The problem depends much on how we heat up the air. If it's so fast, Hg will come out very quickly (Hg gains a lot of kinetic energy in this case). But for simplicity, just assume that we heat up the air VERY SLOWLY. That means, at every point of time, the system is in equilibrium: the pressure by the air balances out the weight of Hg and the ambient pressure (in this case, Hg gains negligible amount of kinetic energy; it flows out very slowly).

We have 2 equations:
_ From the condition of heating slowly: P = \rho g(L-x) + P_o

_ For ideal gas approximation: \frac{Px}{T}=const=\frac{P_1x_1}{T_1}=C

Therefore: T = \frac{\rho g}{C}(L-x)x + \frac{P_o}{C}x

So you have T(x) or T(V). The interesting thing is, under certain circumstances, you can show that you don't have to heat the air up until Hg all flows out in order to push all Hg out. I'll leave it for you to find out You can do further analysis on what will happen in that case, if you want

 

[Tusike]

Great, thanks; that explanation was exactly what I was looking for.

As for you're question, I'm not sure yet what you mean. Perhaps if P0 is small enough, the pressure of the air will decrease in a much greater rate, allowing the volume to expand much easily? I haven't had time to look into it, but it's just a guess.

 

[hikaru1221]

Great, thanks; that explanation was exactly what I was looking for.

As for you're question, I'm not sure yet what you mean. Perhaps if P0 is small enough, the pressure of the air will decrease in a much greater rate, allowing the volume to expand much easily? I haven't had time to look into it, but it's just a guess.

Ambient pressure is almost the same everywhere, so we cannot adjust it
So far we are still with the assumption that the process takes place SLOWLY. The volume still expands, even though it's slow.
A bit mathematical analysis on the function T(x) will lead to the answer