Thermodynamics.... Constant volume pressure of combustion

[Chestermiller]

Thoughts... It's new territory for me. I'm having to look up a lot of the things you're mentioning to properly understand them, so I'm not quite eye to eye with you yet. Still a day or two worth of posts behind on the learning curve.

However, I have used equations for Adiabatic Compression in the past, to calculate pressures and temperatures after turbo and super charging. Instead of assuming some average value for $\gamma$, couldn't we calculate the actual average?

I'll take your word for it, that it's crude. As crude as it may be, do you think that doing it that way would at least indicate an air/fuel ratio that creates the most possible pressure accurately, even though the accuracy of the final temperature and pressure may questionable?

Stated another way...
If my hunch is true, that rich makes more pressure, will doing it that way indicate accurately which fuel ratio is capable of creating the best pressure, no matter what the calculations say that pressure is?

What's the best method to identify the ratio that makes the most pressure (without worrying about how accurate the calculated pressure is)?

That's all I want to calculate. If easy and crude will do that, let's do that.

We would have to spot check it against the more accurate calculation on a few cases to be sure. That's the only way I know of.

If we employ Option 2 (i.e., regarding the product gas as an ideal gas mixture), then we can calculate an average gamma over the range of temperatures from T3 to T4 as follows:

$$\bar{\gamma}_{3,4}=\frac{\sum{y_i}\left[\int_{T_3}^{T_4}{C_{p,i}(T)\frac{dT}{T}}\right]}{\sum{y_i}\left[\int_{T_3}^{T_4}{C_{p,i}(T)\frac{dT}{T}}\right]-R\ln{(T_4}/T_3)}=\frac{\sum{y_i}(I_i(T_4)-I_i(T_3))}{\sum{y_i}(I_i(T_4)-I_i(T_3))-R\ln{(T_4}/T_3)}\tag{1}$$where $$I_i(T)=\int_{T_{Ref}}^{T}{C_{p,i}(T')\frac{dT'}{T'}}\tag{2}$$and where $T_{Ref}$ is any specified reference temperature, and $y_i$ is the mole fraction of species i, and $C_{p,i}(T)$ is the ideal gas molar heat capacity of species i at temperature T. For convenience, values of the integral in Eqn. 2 are tabulated in Moran et al are tabulated for CO2, H2O, O2, and N2 up to temperatures of 3250 K. At higher temperatures, we need to continue the integration on our own. Eqn. 1 must be solved simultaneously with the equation: $$\frac{T_4}{T_3}=\left(\frac{V_3}{V_4}\right)^{(\bar{\gamma}_{3,4}-1)}\tag{3}$$ to get the final temperature $T_4$. The final pressure can then be obtained from the ideal gas law.

 

[Chestermiller]

Step 4 Continued:

There is a simple way of taking into account the non-ideality of the gas behavior of step 4, by approximating the P-V-T behavior of the gas using the van-der-Waals equation of state: $$P=\frac{nRT}{V-nb}-\frac{an^2}{V_2}$$ where the constants a and b describe the deviations from ideal gas behavior; a and b are physical properties of the individual species that are tabulated in the literature. I'm not going to go into the details, but, if the various species are described by the van der Waals equation, the results of the previous section become:$$\frac{T_4}{T_3}=\left(\frac{V_3}{V_4-nb}\right)^{(\bar{\gamma}_{3,4}-1)}\tag{3}$$ for the final temperature and $$P_4=\frac{nRT_4}{V_4-nb}-\frac{an^2}{V_4^2}\tag{2}$$ for the final pressure, with $$a=\left(\sum {y_i\sqrt{a_i}}\right)^2\tag{3}$$and $$b=\left(\sum {{y_ib_i}}\right)\tag{4}$$Eqns. 3 and 4 are empirically derived mixing rules for a combination of gases obeying the van der Waal equation of state.

 

[InquisitiveOne]

Seems that you're enjoying the challenge of figuring this out too. I'm really happy to have someone so capable helping to figure this out with me. Thank you Chet. I'm still not up to speed yet and getting somewhat lost in some of the calculations. I'll post up some specific questions in the coming week.

-Seth-

 

[RodRico]

I was in a similar situation as you InquisitiveOne; I'm an Electrical/Systems Engineer who has undertaken design of an HCCI engine and has had to learn all this material just as you have.

Let me start my answering your question, "The ultimate reason behind my trying to figure this out is, engines make more horsepower with richer than stoichiometric conditions. For instance, gasoline makes peak torque/power at a ratio close to 12.5:1, when stoichiometrically all the oxygen is gone at 14.7:1. Why is that?"

I like addressing this point from the perspective of HCCI in which a pre-mixed fuel/air mixture is compressed to ignition. In this approach, it's easy to imagine that each molecule of fuel is surrounded by air sufficient to combust that molecule and the mixture compressed to yield the heat necessary to initiate the reaction. In this ideal state, the optimum air/fuel ratio would be stoichiometric. The air/fuel mixture is not, however, perfectly mixed; it has local rich and lean regions. The variance in mixture homogeneity is accommodated according to objective. If the objective is maximum power, then excess fuel is provided to ensure all the air is consumed. If the objective is maximum fuel efficiency, excess air is provided to ensure all fuel is consumed.

Moving on to calculations...

The calculation of atmospheric (ambient) conditions is described at https://www.grc.nasa.gov/WWW/K-12/airplane/atmosmet.html

The fundamental calculations for Pressure (Pa), Volume (m3), and Temperature (K) are the isentropic functions given at https://en.wikipedia.org/wiki/Isentropic_process#Table_of_isentropic_relations_for_an_ideal_gas

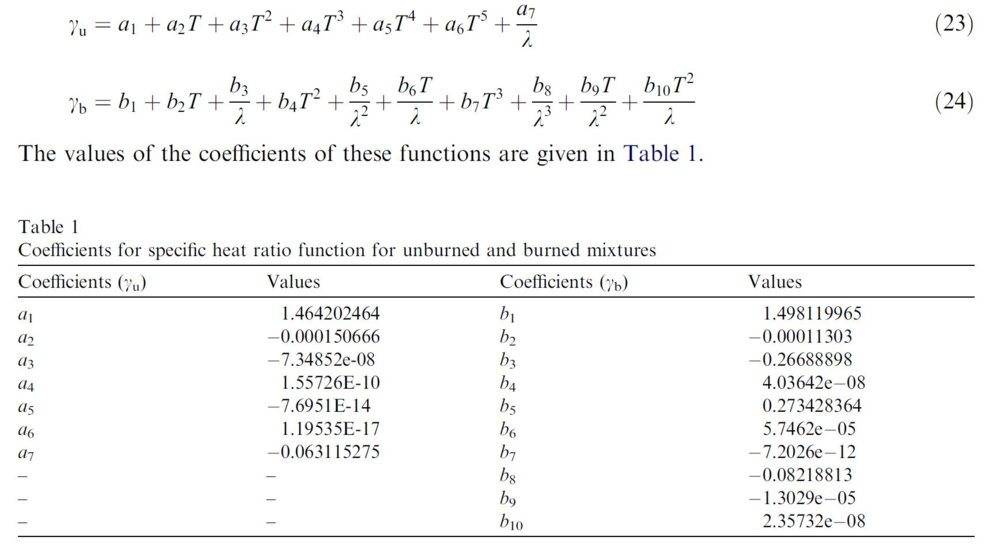
The critical specific heat ratio (y) varies with temperature and mixture composition. The paper "https://www.researchgate.net/publication/222535464_Temperature_and_air-fuel_ratio_dependent_specific_heat_ratio_functions_for_lean_burned_and_unburned_mixture" provides a pretty good summary of the variance in y depending on temperature and mixture composition. Below is a snapshot of the key section giving the equation for y when the mixture is unburned (yu) and burned (yb) where T is temperature (K) and λ is the air-fuel ratio. Note the equaton for pure air is available on-line.

Given all the above, you can create an Excel spreadsheet that starts with atmospheric conditions in the intake volume from which you can calculate mass via PV=mRT where P is in Pa, V is in m3, m (mass) is in kg, R is 286.98 and T is in K. Next, make a table of V values between initial and compression V noting that compression V/initial V is the compression ratio. If you wish, the compression V can also be calculated from a target pressure or temperature with good reason (more later).

A critical equation for calculating energy and work is Q=mCvΔT where Q is Joules, m is mass in kg, Cv is 286.98/(y-1) and ΔT is the change in temperature from one step to the next. This equation can be applied to each step in the table described in the prior paragraph to determine how much energy was added to the closed volume through compression. Conversely, it shows the amount of work done on the gas during compression. Since we're going to focus on work, we want negative values during compression, so subtract the higher temperature from the lower temperature when determining ΔT.

The Q=mCvΔT equation is also used to determine heat added by fuel during combustion. In this case, m (mass) is the kg of fuel added and Q is Joules-per-kg of the fuel according to it's Lower Heating Value (LHV) (43.4 MJ/kg for gasoline). From this, ΔT can be calculated then added to the temperature at the end of compression to find the temperature after combustion. See later notes on accuracy.

Once the combustion temperature is known, the isentropic relations and y can be used to calculate the associated rise in pressure. Using the now known Volume, Pressure, and Temperature, you can build a second table similar to the first that expands the gas. The work done during this phase is also calculated with the Q=mCvΔT equation but with positive (work output) results.

Once both tables are complete, you can calculate Work in Joules by summing the work columns from the Compression and Expansion tables. Using RPM and knowledge of your cycle (i.e. 4 vs 2 stroke), you can convert the sum to Joules per minute (J/min). Finally, you can convert J/min to HP using an on-line calculator.

Now about accuracy...

A key error source not described is friction. It can be estimated using the figure below that I compiled from two key sources, Ricardo and Heywood. The figures are for a 6 cylinder engine. To use this data, you'll have to calculate HP the way professionals do using IMEP, FMEP, and BMEP: IMEP (bar) = Work (J)/Displacement (m3), FMEP (bar) from the figure below, and BMEP (bar) = IMEP-BMEP. Once you have BMEP, the calculations at http://www.epi-eng.com/piston_engine_technology/bmep_performance_yardstick.htm and a few unit conversions can be used to calculate HP and Torque (lb-ft).

The largest single error source in the model as described is heat loss which accounts for a very large part of efficiency losses. It can be approximated by assuming the cooling system holds the cylinder at around 400K (to prevent breakdown of the lubricating oil) then working through the equation at https://www.engineeringtoolbox.com/convective-heat-transfer-d_430.html using one of the heat transfer coefficients given on page 147 - 149 of the document at http://www.ni.com/pdf/manuals/NICASUM.pdf (the model being described here is so course, it really doesn't matter which one is selected). The larger issue in calculating heat loss (and another key loss, pumping loss) is the fact that it assumes knowledge of engine geometry (areas, piston speeds, etc.) which requires some pretty intense work to develop.

There is some small work done during exhaust and intake. These processes are not performed on a closed volume, so the calculation of work is different than that given (left as an exercise). Assuming properly sized valves that don't produce excess pumping loss, the primary reason for incorporating the intake and exhaust cycles is to capture their impact on heat transfer; in the prior discussion, for example, conditions at the start of compression were assumed to be ambient (typically 288K at sea level) but it's clear that contact with the 400K typical wall during intake will in fact warm the charge and affect the start condition of compression.

The method I described for calculating temperature after combustion is very coarse because it assumes all the heat of the fuel was released instantaneously. Only HCCI comes close to releasing the fuel heat so quickly (illustrated in the video below); Spark engines depend on comparatively slow flame propagation and diesel engines depend on the time required for spray injection and the kinetics of air and fuel mixing in that spray (to make matters worse, the use of crankshafts means the volume is changing during heat release, so the slower spark and diesel systems aren't actually operating using fixed volume combustion, and this impacts all the calculations). The heat release rate of the selected combustion technique combined with the ignition delay associated with octane factors heavily into timing as previously noted.

Some practical considerations...

In the Otto cycle, the peak compression temperature of the air/fuel mixture must be limited such that the bulk of heat release occurs after Top Dead Center. The timing of combustion is affected by ignition delay which is affected by octane in turn. Furthermore, the mechanical efficiency of the linear to rotary conversion system (typically a crankshaft) has some bearing on the timing of heat release. It's all quite complex.

In all cycles, peak combustion pressure must be held below around 220 bar or the lubricating oil in the cylinder and rings will auto-ignite. This phenomenon is a hot topic in design of modern turbo charged engines and, in this realm, it's called Low Speed Pre-Ignition (LSPI). You will find that this 220 bar limit sets the upper temperature limit of combustion. As a result, you will find that greater compression leaves less ΔT for generation by fuel, and this reduces power.

All modern engines use catalytic converters, and they require a minimum exhaust temperature around 533K. Ignoring heat loss, compression and expansion in an Otto cycle engine are inversely correlated, so at least 533K of heat must be added by fuel to meet this requirement.

I hope all this helps!

Rod