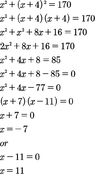Three Consecutive Odd Integers

  • Context: MHB 
  • Thread starter Thread starter mathdad
  • Start date Start date
  • Tags Tags
    Integers
Click For Summary
SUMMARY

The discussion focuses on finding three consecutive odd integers where the sum of the squares of the first and third equals 170. The correct equation is established as x² + (x + 4)² = 170, where x represents the first odd integer. Participants emphasize the importance of ensuring that x remains odd, suggesting the substitution x = 2n + 1 as a method to enforce this condition. Corrections are made regarding the signs in the polynomial expansion, leading to the final form (x - 7)(x + 11) = x² + 4x - 77.

PREREQUISITES
  • Understanding of algebraic equations and polynomials
  • Knowledge of properties of odd integers
  • Familiarity with solving quadratic equations
  • Basic skills in mathematical substitutions
NEXT STEPS
  • Practice solving quadratic equations with real-world applications
  • Explore the properties of odd and even integers in algebra
  • Learn about polynomial factorization techniques
  • Investigate mathematical problem-solving strategies for integer sequences
USEFUL FOR

Students, educators, and anyone interested in enhancing their algebraic problem-solving skills, particularly in the context of integer sequences and quadratic equations.

mathdad
Messages
1,280
Reaction score
0
Find three consecutive odd integers such that the square of the first plus the square of the third is 170.

See picture for the set up.

View attachment 7356

Is the set up correct?
 

Attachments

  • MathMagic171010_2.png
    MathMagic171010_2.png
    2.2 KB · Views: 127
Last edited by a moderator:
Mathematics news on Phys.org
Re: Three Executive Odd Integers

RTCNTC said:
Find three consecutive odd integers such that the square of the first plus the square of the third is 170.

See picture for the set up.

Is the set up correct?
That's good. Just solve for x and make sure your answer is odd. Another addition to this would be to set x = 2n + 1, which forces x to be odd, but you don't actually have to take this step.

-Dan

Edit: Whoops! Your equation should only contain two numbers: [math]x^2 + (x + 4)^2 = 170[/math]. Sorry about that.
 
Re: Three Executive Odd Integers

topsquark said:
That's good. Just solve for x and make sure your answer is odd. Another addition to this would be to set x = 2n + 1, which forces x to be odd, but you don't actually have to take this step.

-Dan

Edit: Whoops! Your equation should only contain two numbers: [math]x^2 + (x + 4)^2 = 170[/math]. Sorry about that.

Ok. Thanks.
 

Attachments

  • MathMagic171010_1.png
    MathMagic171010_1.png
    10.3 KB · Views: 115
Last edited by a moderator:
Re: Three Executive Odd Integers

RTCNTC said:
See picture reply.

Correct?
You switched signs. It's [math](x - 7)(x + 11) = x^2 + (-7 + 11)x - 77 = x^2 + 4x - 77[/math].

-Dan
 
Re: Three Executive Odd Integers

I rushed through the problem. Thanks for the correction.
​
 

Similar threads

MHB What Are the Consecutive Even Integers in This Algebra Problem?
  • · Replies 7 ·
Replies
7
Views
2K
High School Square Root of an Odd Powered Integer is Always Irrational?
  • · Replies 31 ·
2
Replies
31
Views
4K
Undergrad Proof of Differences of Odd Powers
  • · Replies 11 ·
Replies
11
Views
2K
MHB Set of 2015 Consecutive Positive Ints with 15 Primes
  • · Replies 3 ·
Replies
3
Views
2K
MHB Largest Even Integer: Impossible Sum of Two Odd Composites
  • · Replies 2 ·
Replies
2
Views
1K
MHB Prove f(n) is a product of two consecutive positive integers for all n
  • · Replies 1 ·
Replies
1
Views
1K
MHB Find the number of pairs of consecutive integers
  • · Replies 4 ·
Replies
4
Views
3K
Sides of a triangle
  • · Replies 16 ·
Replies
16
Views
2K
Graduate Are There More Integer Solutions to a^3+b^3+c^3=d^3 Beyond 3^3+4^3+5^3=6^3?
  • · Replies 2 ·
Replies
2
Views
4K
Undergrad Odd/even functions and fractional indices
  • · Replies 28 ·
Replies
28
Views
5K