kamil.borkowski
- 8
- 0
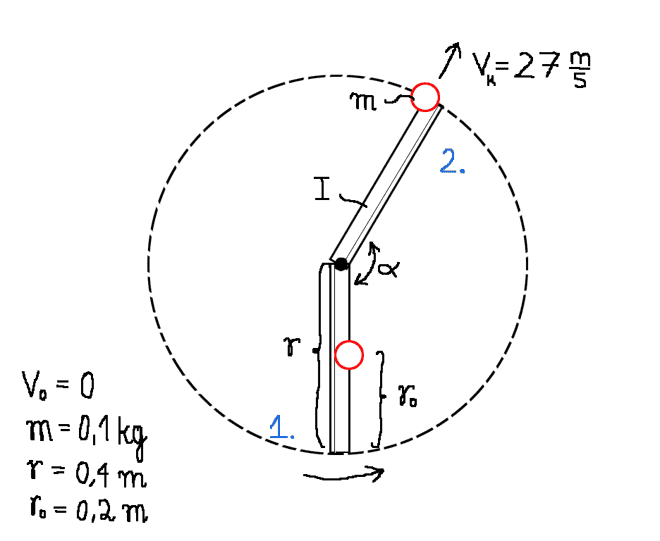
Hi! I need a help in desiging a target thrower. I can't find a force that is needed in order to throw a target with certain velocity. I assume that it's going to be a centrifugal force, but I can't find a connection with linear movement of target and rotation of an arm. Does anyone have an idea? Here's a picure: