Time Dilation Formula: Clarifying Confusion

[Grimble]

How do you think the light clock thought-experiment applies these rules "across frames"? The light clock thought-experiment derives the slowed down rate of ticking of the moving light clock using only a single frame, namely the frame in which the light clock is moving--the derivation only uses velocities and distances and times which are measured in the coordinates of that frame.

Do you understand that just because I am observing a clock which is moving relative to myself, does not mean that I need to use any frames other than my own rest frame to analyze its behavior? That talking about the properties of an object which is moving relative to me (like the time on a moving clock) does not in any way imply I am comparing multiple frames, I can analyze these properties just fine using nothing but my own rest frame? A frame is just a coordinate system after all, I can perfectly well keep track of the way the position coordinate of the moving object changes with coordinate time using just the coordinates of my rest frame.

I'm sorry if I am getting confused here, but as I have just said in my last post I was visualising this as Einstein's embankment and moving train where he thought it necessary to use separate co-ordinate frames. Was he over complicating it when he could have worked it all in relation to the embankment, is that what you are saying? Or am I becoming confused again?

It does seem to be complicated and confusing, when discussing these things, to agree on what we are intending to convey. Oh the complexities of language and syntax!

Grimble

 

[Grimble]

You bolded the second half of my sentence but then ignored the first half, taking the meaning out of context. I first said "In this case we are dealing with two clocks that have different velocities in frame B, but we are measuring both their ticking rates from the perspective of frame B"--so when I then said "nothing about the 1st postulate suggests that their ticking rates should be identical", I was clearly talking about their ticking rates in frame B, not their ticking rates in their own respective rest frames. Hopefully you'd agree that nothing about the first postulate suggests that their ticking rates should be identical in frame B, given that one is at rest in frame B and the other is not?

Mea Culpa! once again.

The bolding in the above quoted post was unintentional, and I hadn't realized it had happened until you pointed it out; it was completely unintentional and changed the whole meaning of my reply SORRY!

I do certainly agree that they would have different rates of ticking when measured from the same frame.

Grimble

 

[Ich]

I have been picturing the stationary clock as being placed on Einstein's embankment and the moving clock riding on his train; am I misreading this situation?

Didn't you talk abouthttp://www.pa.msu.edu/courses/2000spring/PHY232/lectures/relativity/contraction.html" ?

As for speed, I take that as non-directional (for speed with direction is velocity?) and it is distance/time.

Yes, distance/time if both are measured in the same reference frame. See the difference to your statements?
Things should become a lot clearer if you know and use the definition of the standard terms. Carry on with the diagrams.

 

[JesseM]

I'm sorry if I am getting confused here, but as I have just said in my last post I was visualising this as Einstein's embankment and moving train where he thought it necessary to use separate co-ordinate frames. Was he over complicating it when he could have worked it all in relation to the embankment, is that what you are saying? Or am I becoming confused again?

Einstein wasn't analyzing time dilation in the train/embankment thought-experiment, he was analyzing the relativity of simultaneity, and since the relativity of simultaneity is all about how simultaneity differs between two frames of course he needed to look at the thought-experiment from the perspective of both frames. But that doesn't mean every analysis of a moving object requires multiple frames.

Again, do you understand the difference between talking about an object moving relative to you and talking about a frame moving relative to you? If I am at rest on the embankment, I can perfectly well analyze the behavior of a moving train, or a moving light clock aboard the train, using only the embankment frame, without ever making reference to the train's own rest frame--do you disagree with that? If not, note that this is in fact the sort of thing I did with the moving light clock, figuring out the time between ticks using only the observer's frame, not the light clock's own rest frame. And if you do disagree, please address this previous post:

If you think any frames other than the observer's rest frame are used in analyzing the light clock, can you point out the specific step in the analysis where you think this happens? For example, do we need any frames other than the observer's frame to figure out the distance the mirrors have traveled horizontally in a given time if we know their velocity v? Do we need any frames other than the observer's frame to use the pythagorean theorem to figure out the diagonal distance the light must travel if we know the horizontal distance traveled by the mirrors (just v*t, where t is the time between the light hitting the top and bottom mirror and v is the horizontal velocity of the mirrors) and the vertical distance h between them? Do we need any frames other than the observer's frame to figure out the time T that would be required in order to ensure that the diagonal distance D = \sqrt{v^2 T^2 + h^2} will satisfy D/T = c? (making use of the second postulate which says light must move at c in every frame, including the observer's frame, along with the ordinary kinematical rule that speed = distance/time)

From all this, you can conclude that the time T between ticks of the light clock in the observer's frame must be equal to T = \frac{h}{\sqrt{c^2 - v^2}}. Only here do you have to consider another frame if you want to derive the time dilation formula from this--you have to figure out what the time t between ticks would be in the light clock's own rest frame, and obviously if h is the vertical distance between mirrors this would be t = h/c (here you do need to make an argument to show the vertical height h will be the same in both frames, that there will be no length contraction perpendicular to the direction of motion). Then if you divide T/t you get the gamma factor \frac{1}{\sqrt{1 - v^2/c^2}}. But this is just simple division, when deriving the time between ticks in each frame you can work exclusively with the coordinates of that frame and not worry about other frames.

 

[Grimble]

Didn't you talk abouthttp://www.pa.msu.edu/courses/2000spring/PHY232/lectures/relativity/contraction.html" ?

Yes, but surely this is the equivalent of http://www.bartleby.com/173/7.html" where Einstein writes:

The velocity W of the man relative to the embankment is here replaced by the velocity of light relative to the embankment. w is the required velocity of light with respect to the carriage, and we have
w = c - v.
The velocity of propagation of a ray of light relative to the carriage thus comes out smaller than c.
But this result comes into conflict with the principle of relativity set forth in Section V. For, like every other general law of nature, the law of the transmission of light in vacuo must, according to the principle of relativity, be the same for the railway carriage as reference-body as when the rails are the body of reference. But, from our above consideration, this would appear to be impossible. If every ray of light is propagated relative to the embankment with the velocity c, then for this reason it would appear that another law of propagation of light must necessarily hold with respect to the carriage—a result contradictory to the principle of relativity.

And don't worry I am continuing with my diagrams. (This is all fascinating!)

 

[Grimble]

Again, do you understand the difference between talking about an object moving relative to you and talking about a frame moving relative to you? If I am at rest on the embankment, I can perfectly well analyze the behavior of a moving train, or a moving light clock aboard the train, using only the embankment frame, without ever making reference to the train's own rest frame--do you disagree with that?

Not at all,

If not, note that this is in fact the sort of thing I did with the moving light clock, figuring out the time between ticks using only the observer's frame, not the light clock's own rest frame.

as indeed Galileo and Newton would have done! But what has it to do with SR?

Let me address the previous post you quote.

We have the horizontal distance = vT,
The vertical distance h (which, if the clock is ticking seconds in this frame = 1 x c)
and the diagonal distance D, where D = \sqrt{{v^2}{T^2} + {h^2}}

And you quite rightly say that only one frame is needed to reach this point. In fact it could be done using either frame.
Consider, if you will, that if we were to use the light clock's own frame of reference, then we should still say that the oberver, traveling at v relative to the clock would still see the diagonal D = \sqrt{{v^2}{T^2} + {h^2}}.

I have no problem with this at all, nor with the conclusion that:
T is the time for light to travel from the mirror to the observer while
t is the time for the light to travel back to the source
and that if the clock is ticking seconds in its own frame of reference then it will take γ seconds, measured in that same frame, to reach the observer.

But the first postulate also requires that an identical clock in the oberver's frame of reference would also be ticking seconds, identical seconds as they are both inertial frames of reference, or Galilean frames as Einstein termed them.

What we have to determine here, is how to resolve the difference in what the observer sees, between the time in his own frame of 1 second and that he observes in the clock's frame of γ seconds.

Thankfully Einstein gave us the way of doing this:
We transform the time observed in the clock's frame using the Lorentz Transformation, and thus we find that T, in transformed units( in order to avoid any dispute over exactly what we are referring to I shall refer to them as transformed units and inertial units) is equal to 1 second inertial time.

But if T inertial seconds = γ seconds in (inertial) time, then

T in transformed seconds = γ seconds in transformed time
yet
T in transformed seconds = 1 second in inertial time
therefore
γ seconds in transformed time = 1 second in inertial time

or in the more usual terms used {t^'} = \frac{t}{\gamma} which is what we should expect as it reflects the analagous formula for length contraction {L^'} = \frac{L}{\gamma} from which we can see that if c = \frac{L}{t} then c = \frac{L^'}{t^'} which of course it has to do.

Now one last little consideration:

If we say that v = 0.866c then \gamma = 2 and if we apply this to our scenario above
we find that the time for light to traverse the diagonal path = \gamma = 2 seconds inertial time = 2\gamma (or {\gamma^2}) = 4seconds transformed time
and the corresponding diagonal distance will be 4 transformed light seconds
so the observer, observing the clocks reference frame will see the light take 4 transformed seconds to cover the 4 transformed light seconds; that is the equivalent of 2 seconds to cover 2 lightseconds inertial time. (all at the speed of c)

And if you have followed all my ramblings you can see that everything adds up and matches up.
I.e. the clock ticks once a second for both the observer and the clock. In the clocks frame of reference the light will take two seconds to reach the observer, but to the observer, observing the clocks frame of reference it will take 4 transformed seconds!

All as neat and tidy as Einstein could have wished.

 

[JesseM]

as indeed Galileo and Newton would have done! But what has it to do with SR?

Galileo or Newton would not have assumed that the light must be traveling at c in both their own frame and the clock's rest frame--in fact they would have assumed that if it is traveling at c in one of those frames, it must be traveling at a different speed in the other frame, in such a way that both frames end up agreeing on the time between ticks.

Let me address the previous post you quote.

We have the horizontal distance = vT,
The vertical distance h (which, if the clock is ticking seconds in this frame = 1 x c)
and the diagonal distance D, where D = \sqrt{{v^2}{T^2} + {h^2}}

And you quite rightly say that only one frame is needed to reach this point. In fact it could be done using either frame.
Consider, if you will, that if we were to use the light clock's own frame of reference, then we should still say that the oberver, traveling at v relative to the clock would still see the diagonal D = \sqrt{{v^2}{T^2} + {h^2}}.

I have no problem with this at all, nor with the conclusion that:
T is the time for light to travel from the mirror to the observer while
t is the time for the light to travel back to the source
and that if the clock is ticking seconds in its own frame of reference then it will take γ seconds, measured in that same frame, to reach the observer.

OK, so we agree that the time between ticks for the moving light clock can be derived using only the observer's frame. Then as I pointed out in that earlier post, if you want to derive the time dilation equation which compares time in the clock's rest frame to time in the observer's frame, that's when you do have to bring in some assumptions about multiple frames:

From all this, you can conclude that the time T between ticks of the light clock in the observer's frame must be equal to T = \frac{h}{\sqrt{c^2 - v^2}}. Only here do you have to consider another frame if you want to derive the time dilation formula from this--you have to figure out what the time t between ticks would be in the light clock's own rest frame, and obviously if h is the vertical distance between mirrors this would be t = h/c (here you do need to make an argument to show the vertical height h will be the same in both frames, that there will be no length contraction perpendicular to the direction of motion). Then if you divide T/t you get the gamma factor \frac{1}{\sqrt{1 - v^2/c^2}}. But this is just simple division, when deriving the time between ticks in each frame you can work exclusively with the coordinates of that frame and not worry about other frames.

The assumption that the vertical height between mirrors is the same in both frames does involve thinking about multiple frames in SR, as does the assumption that if the height is h in the clock's rest frame, the time between ticks must be t = h/c in that frame.

What we have to determine here, is how to resolve the difference in what the observer sees, between the time in his own frame of 1 second and that he observes in the clock's frame of γ seconds.

You have it backwards here. The time in the observer's frame will be the greater time, not the lesser time (and the gamma factor γ is always greater than 1). So, if the time in the clock's frame is 1 second, the time in the observer's frame will be gamma seconds (and if the time in the clock's frame is T seconds, the time in the observer's frame is T*gamma seconds)

We transform the time observed in the clock's frame using the Lorentz Transformation, and thus we find that T, in transformed units( in order to avoid any dispute over exactly what we are referring to I shall refer to them as transformed units and inertial units) is equal to 1 second inertial time.

That's not good terminology, since both frames are "inertial" ones in the terminology of relativity. Also it's not as if the time in the observer's frame is intrinsically the one that's been "transformed", you can equally well start out with the time in the observer's frame and then use the Lorentz transformation to derive the time in the clock's frame. Better terminology would just be to give names to the two frames, like "clock's frame" and "observer's frame", or just use different notation to refer to them like unprimed t vs. primed t'.

But if T inertial seconds = γ seconds in (inertial) time, then

What? I thought you were using "inertial" time to refer to time in the clock's frame, but the time in the clock's frame cannot be both T seconds and gamma seconds. If the time between ticks of the clock in the clock's frame is T seconds, then the time between ticks of that same clock in the observer's frame (what you were calling 'transformed' time) would be gamma*T seconds.

T in transformed seconds = γ seconds in transformed time
yet
T in transformed seconds = 1 second in inertial time
therefore
γ seconds in transformed time = 1 second in inertial time

Don't understand these either. And why are you using three times--1 second, T seconds, and gamma seconds? If we have only two frames to consider there should be only two times involved. If the time in the clock's frame is 1 second than the time in the observer's frame will be gamma seconds, while if we say more generally that the time in the clock's frame is T seconds (i.e. not assuming the distance between mirrors is 1 light-second), then the time in the observer's frame is gamma*T seconds.

or in the more usual terms used {t^'} = \frac{t}{\gamma}

If t is supposed to be the time in the clock's own rest frame and t' is the time in the observer's frame, then this formula is wrong, you should be multiplying by gamma rather than dividing by it: t' = t * \gamma.

which is what we should expect as it reflects the analagous formula for length contraction {L^'} = \frac{L}{\gamma}

This is the correct formula for length contraction if L is the object's length in its own rest frame and L' is the length in the observer's frame, but you can see that it's not exactly analogous to the correct formula for time dilation I wrote above, the formula for time dilation involves multiplying by gamma while the formula for length contraction involves dividing by gamma.

from which we can see that if c = \frac{L}{t} then c = \frac{L^'}{t^'} which of course it has to do.

Nope, the fact that the speed of light is c in both frames cannot be derived from the length contraction and time dilation formulas alone, you also have to take into account the relativity of simultaneity. See my post here for a numerical example of how to take into account all three factors to show that two frames will both measure a light beam to move at c.

If we say that v = 0.866c then \gamma = 2 and if we apply this to our scenario above
we find that the time for light to traverse the diagonal path = \gamma = 2 seconds inertial time

Again I'm confused--wasn't inertial time supposed to be time in the clock's own rest frame? Why would you use gamma to find that time? If the mirrors are 1 light-second apart, the time in the clock's rest frame will be 1 second, naturally. I suppose you're free to imagine that the mirrors are gamma light-seconds apart in the clock's rest frame, but there's no reason why relativity demands this, the mirrors can be set to any distance apart you wish in the clock's rest frame.

= 2\gamma (or {\gamma^2}) = 4seconds transformed time
and the corresponding diagonal distance will be 4 transformed light seconds

Yes, if the vertical distance between the mirrors happens to be 2 light seconds, and the mirrors are moving at 0.866c in the observer's frame, then the observer will see the diagonal distance as 4 light seconds and the time between ticks as 4 seconds. But again there's no reason why the vertical distance had to be 2 light seconds, you could have equally well said it was some other arbitrary distance like 3.5 light seconds, in which case the time between ticks in the observer's frame would be 2*3.5 = 7 seconds.

so the observer observing the clocks reference frame will see the light take 4 transformed seconds to cover the 4 transformed light seconds; that is the equivalent of 2 seconds to cover 2 lightseconds inertial time. (all at the speed of c)

The observer isn't "observing the clocks reference frame", he's just observing the clock, and measuring it from the perspective of his own inertial frame. He doesn't have to know anything about the Lorentz transformation whatsoever, he can just measure the time between ticks directly using synchronized clocks at rest in his own frame (or else he can figure out what the time between ticks must be given the vertical distance between the mirrors, the speed at which the clock is traveling which allows him to calculate the diagonal distance using the Pythagorean theorem, and the assumption based on the second postulate that the light must move at c in his frame). If he uses a network of synchronized clocks at rest in his frame, then he just has to note the time T1 on a clock of his that was right next to the bottom mirror when the light was emitted ('right next to' so that he is assigning times using only local measurements and he doesn't have to worry about delays between when an event happens and when a signal from the event reaches one of his clocks), and then note the time T2 on a clock of his that was right next to the top mirror when the light reached it, and the time between ticks in the observer's frame will just be T2 - T1. If the two mirrors happen to be 2 light-seconds apart vertically, and the light clock is moving at 0.866c, then T2 - T1 will equal 4 seconds as you say, but you can see that there was no need for the observer to make use of the Lorentz transformation to find this time (although of course it will agree with the time predicted by the Lorentz transformation if you start with the time in the clock's rest frame and then transform into the observer's frame).

 

[Rasalhague]

I've just had a go at making a spacetime diagram of JesseM's example, in post #9 there. This is a traditional Minkowski spacetime diagram in which two inertial frames of reference, with a uniform relative velocity, are superimposed for comparison.

I haven't written c in the calculations because Jesse used units of seconds and light seconds, in which the speed of light is 1 light second per second. 1 light second is a unit of length, defined as how far light travels in 1 second. It's approximately 3 * 10^8 metres, about 3/5 of the way from the Earth to the moon. Using normalised units such as this makes the equations simpler.

Events which lie on the same horizontal line (i.e. any line parallel with the horizontal x axis) with each other are simultaneous in Jesse's rest frame (although not simultaneous in the moving ruler's rest frame).

Events which lie on the same vertical line (i.e. any line parallel with the vertical t(ime) axis) happen in the same place with respect to Jesse's rest frame.

The parallel lines marked with a single slash are the world lines of the ends of what Jesse calls the "moving ruler" (the world lines of the two clocks). An object's world line is its trajectory through spacetime; the world line shows the object's location in space at every instant in time. Because the ends of the moving ruler are, by definition, not moving in the ruler's rest frame, events which happen on one of these lines have the same spatial coordinates (in this ruler's rest frame) as any other events on the same line.

Lines with a double slash are lines of simultaneity in the rest frame of the moving ruler. An event which lies on one of those lines is simultaneous in the moving ruler's rest frame with all other events which lie on that line (although not simultaneous in Jesse's rest frame). Such events have the same time coordinate in the moving ruler's rest frame.

The line labelled "light cone" is the world line of the light. There are two significant events on this world line. The first is the emission of the flash of light from the common spacetime origin (where and when the zero end of the moving ruler coincides with Jesse's). The second is the arrival of the light at the other end of the moving ruler. In the moving ruler's rest frame, this second event is 50 light seconds away from the origin, and happens 50 seconds later in time (according to both of the clocks, as they're synchronised in that frame). In Jesse's rest frame, the second event occurs 100 light seconds away from first and happens 100 seconds later in time. Thus the speed of light is the same in both frames.

Various relevant values are shown in terms of gamma = 1/sqrt(1 - (v/c)^2), which in this case is 1/sqrt(1 - (3/5)^2) = 5/4 = 1.25. I've also shown alternative, equivalent way of calculating these values, using the hyperbolic functions cosh (hyperblic cosine), sinh (hyperbolic sine) and tanh (hyperbolic tangent).

Two values which Jesse didn't mention are the 37.5 seconds and 62.5 light seconds. These are respectively the t and x coordinates in Jesse's rest frame of the event of the clock at the moving ruler's far end showing time = 0. In the ruler's rest frame, this event happens simultaneously with the the event of both clocks showing 0 at the shared spacetime origin (and in the ruler's rest frame therefore has no time component, only a space component of 50 light seconds), but in Jesse's rest frame, as he stands of the spacetime origin, it still lies 37.5 seconds in his future!

I used a slightly different colour for some of the labels round the edge. This has no special significance; it was just to separate them more clearly from labels next to them.

I hope I've got everything right. All criticism welcome!

 

[Rasalhague]

[...] an identical clock in the oberver's frame of reference [...]

Are you clear on the fact that if there are two clocks, each moving with some contant velocity relative to the other, both clocks are in all frames of reference, in the sense that both can be described using the language of special relativity with respect to any inertial frame of reference? I think what you have in mind here is "an identical clock which is at rest in the observer's rest frame" (i.e. an identical clock at rest with respect to this observer, not moving with respect to the observer, at a constant distance from the observer--whether located in the same place as the observer or in any other place, so long as there are no tidal effects of gravity present there).

 

[Grimble]

Are you clear on the fact that if there are two clocks, each moving with some contant velocity relative to the other, both clocks are in all frames of reference, in the sense that both can be described using the language of special relativity with respect to any inertial frame of reference? I think what you have in mind here is "an identical clock which is at rest in the observer's rest frame" (i.e. an identical clock at rest with respect to this observer, not moving with respect to the observer, at a constant distance from the observer--whether located in the same place as the observer or in any other place, so long as there are no tidal effects of gravity present there).

Yes, of course, and thank you, I was being a little slipshod in my language there

Grimble

 

[Grimble]

Thank you, JesseM, I can see from your reply that we are understanding different things from what I write. Let me take your input and see if by, applying what you have pointed out I can re-write my thoughts so that you can understand what I am saying

Let me start by defining the terms I use.
Firstly I do not use the terms primed and unprimed as I have seen these used both ways round and swapped so many times that their use, for me at least, has been compromised;

Inertial units (time and space) are those measured locally (by a local observer within that same frame of reference) in any inertial frame of reference. That they are the same in all inertial frames of reference (Galilean frames) is a demand of the first postulate.

Transformed units (time and space) are those same inertial units, transformed using the Lorentz equations, which is how they will appear when observed from another inertial frame of reference and are a function of their relative velocity.
(I am not saying that one is the clock and the other is the observer, I am saying that those terms are dependent on where they are measured from. They are two separate and distinct scales of measurement that are applied where appropriate)
In order to make it easier to follow I will use the subscripts 'i' and 't' applied to the terms that denote measurements to indicate the units that they are measured in.

Again, do you understand the difference between talking about an object moving relative to you and talking about a frame moving relative to you? If I am at rest on the embankment, I can perfectly well analyze the behavior of a moving train, or a moving light clock aboard the train, using only the embankment frame, without ever making reference to the train's own rest frame--do you disagree with that?

Not at all,

If not, note that this is in fact the sort of thing I did with the moving light clock, figuring out the time between ticks using only the observer's frame, not the light clock's own rest frame.

and Galileo and Newton would have agreed that the increased distance traveled by the light would have meant that the speed of light would have increased but the time would have remained constant (relativity principle = 1st postulate) and they would have agreed that the time would have had to increase if the speed were to remain constant (light speed principle = 2nd postulate)
But Einstein would have said No! We must comply with Both Postulates.

Let me address the previous post you quote.

We have the horizontal distance = vT,
The vertical distance h (which, if the clock is ticking seconds in this frame = 1 x c)
and the diagonal distance D, where D = \sqrt{{v^2}{T^2} + {h^2}}

And you quite rightly say that only one frame is needed to reach this point. In fact it could be done using either frame.
Consider, if you will, that if we were to use the light clock's own frame of reference, then we should still say that the observer, traveling at v relative to the clock would still see the diagonal D = \sqrt{{v^2}{T^2} + {h^2}}.

I have no problem with this at all, nor with the conclusion that:
T is the time for light to travel from the mirror to the observer while
t is the time for the light to travel back to the source
and that if the clock is ticking seconds in its own frame of reference then it will take γ = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} seconds, measured in that same frame, to reach the observer. . . . . . .(1)

But the first postulate also requires that an identical clock, stationary in the observer's frame of reference would also be ticking seconds, identical seconds, as they are both inertial frames of reference, or Galilean frames as Einstein termed them. . . . . . .(2)

What we have to determine here, is how to resolve the difference in what the observer sees, between the 1 second that his own identical clock takes to tick and the γ seconds that he observes the moving clock take for each tick.

You have it backwards here. The time in the observer's frame will be the greater time, not the lesser time (and the gamma factor γ is always greater than 1). So, if the time in the clock's frame is 1 second, the time in the observer's frame will be gamma seconds (and if the time in the clock's frame is T seconds, the time in the observer's frame is T*gamma seconds)

But we have just established those times in (1),(2) above!

Thankfully Einstein gave us the way to resolve the difference in what the observer sees,:
We transform the time observed in the clock's frame using the Lorentz Transformation, and thus we find that T, in transformed units is equal to 1 second inertial time. . . . . . (3)
(And remember, I am not saying that one is the clock and the other is the observer, I am saying that those terms are dependent on where they are measured from. They are two separate and distinct scales of measurement that are applied where appropriate)
Yes, indeed, one could take the time from any inertial frame (they are all, by definition equal, after all) and transform it (transformed time being that in one frame viewed from another).

But, in the initial scenario and using only one frame, Ti seconds = γti seconds in time( where γ or \frac{1}{1-\frac{v^2}{c^2}} is the ratio of the distance between the mirrors and that from the mirror to the observer, the diagonal distance), then
{T_t} = \gamma {t_t} seconds in transformed time ...by just changing the units
and as we shewed above in (3)
{T_t} = {t_i} seconds ininertial time (and t, one tick of our clock, = 1)
therefore
γ seconds in transformed time = 1 second in inertial time
i.e. γ is the conversion factor between inertial and transformed units.

So, to reiterate, 1 second inertial time (the observer's own clock) is equal to the time T for the moving clock which is in transformed units and, therefore, to γt seconds transformed units.
But T = 1 giving 1 second inertial time = γ seconds transformed time

or in the more usual terms used {t^'} = \frac{t}{\gamma}

If t is supposed to be the time in the clock's own rest frame and t' is the time in the observer's frame, then this formula is wrong, you should be multiplying by gamma rather than dividing by it: {itex] {t^'} = t*\gamma[/itex].

I have seen the time dilation formula written (and used) in both forms:

1) {t^'} = t * \gamma

2) {t^'} = \frac{t}{\gamma}

1) is the more commonly used but my research indicates that it is 2) that is the correct one for the following reasons:

1. It is the one Einstein formulated;
2. It is the one derived from the Lorentz equations;
3. The 'light clock' derivation is incomplete (as I am shewing in this thread) and reverses the correct derivation;
4. A http://www.answers.com/topic/special-relativity#Time_dilation_and_length_contraction" reverses the terms and thereby reverses the derived formula;
5. Einstein himself, proved
   "[URL="[PLAIN]http://www.bartleby.com/173/11.html"[/URL] that {x} = c{t} and that {x^'} = c{t^'} so the formulae for Length contraction and time dilation have to be analagous or these two equations cannot both be correct;
6. Minkowski space time shews quite conclusively exactly how length contraction and time dilation are, in fact, the same process and could, incidentally, have been termed 'length dilation' and 'time contraction' and all those terms would have been correct! (I will shew this later).

which is what we should expect as it reflects the analagous formula for length contraction {L^'} = \frac{L}{\gamma}

This is the correct formula for length contraction if L is the object's length in its own rest frame and L' is the length in the observer's frame, but you can see that it's not exactly analogous to the correct formula for time dilation I wrote above, the formula for time dilation involves multiplying by gamma while the formula for length contraction involves dividing by gamma.

But no it doesn't, just because someone at sometime in the distant past decided to use the labels length-contraction and time-dilation implying one increases while the other decreases people have been making the mistake of thinking the formulae are opposites, while they are in fact analagous.

from which we can see that if c = \frac{L}{t} then c = \frac{L^'}{t^'} which of course it has to do.

Nope, the fact that the speed of light is c in both frames cannot be derived from the length contraction and time dilation formulas alone, you also have to take into account the relativity of simultaneity. See my post here for a numerical example of how to take into account all three factors to show that two frames will both measure a light beam to move at c.

Yet Einstein did it directly from the Lorentz transformation formula, very simply. It isn't complicated. See paragraph 6

Grimble

 

[Rasalhague]

Inertial units (time and space) are those measured locally (by a local observer within that same frame of reference) in any inertial frame of reference. That they are the same in all inertial frames of reference (Galilean frames) is a demand of the first postulate.

What do you mean by "local"? The "same frame of reference" as what? What you you mean by "in the same frame of reference [...] in any inertial frame of reference"?

The first postulate, in the form Einstein originally presented it, says only that the laws by which the states of physical systems change don't depend on which of two frames, in uniform translatory motion relative to one another, these changes of state are referred to. There's no mention here of either frame being valid only at some location or in some region. It may be necessary for practical purposes to limit the scope of a frame to a specified region of spacetime, small enough for the tidal effects of gravity to be undetectable to whatever instruments are available, but these thought experiments used to introduce the concepts of special relativity leave aside such practicalities and assume that there's no significant gravity. They do this to illustrate effects due only to differences in relative motion of inertial reference frames. In Minkowski spacetime, there's no limit to the size of a reference frame. All frames extend through all spacetime, but the time and space components of vectors are certainly not the same in all inertial frames; they're different in frames moving at different relative velocities. What stays the same is the magnitude of vectors, such as the spacetime interval, and the physical laws themselves. It's only by acknowledging that the individual components of vectors change that the laws themselves can comply with this postulate.

Transformed units (time and space) are those same inertial units, transformed using the Lorentz equations, which is how they will appear when observed from another inertial frame of reference and are a function of their relative velocity.

Do you mean to distinguish between input (source) and output (target) of the transformation? When the space and time components of vectors are changed by the Lorentz transformation, the new space and time components are simply the space and time components of the vector referred to another, equally valid, inertial reference frame. All frames involved here are inertial: both input and output. For this reason, I find the distinction "inertial" versus "transformed" (which you admit is also inertial) confusing.

(I am not saying that one is the clock and the other is the observer, I am saying that those terms are dependent on where they are measured from.

The value of the Lorentz transformation is not dependent on where the inputs are measured from! You could picture each frame, as Taylor and Wheeler do, as an infinite grid of clocks connected by meter-long bars. One frame passes through another, but they occupy the same space. Or you could imagine a single observer recording events at a distance, in which case they'd have to take into account the time it takes for signals to reach them. The Lorentz transformation deals with the differences in time and space as referred to inertial reference frames which differ only in that they're moving at constant velocity in different directions. It deals with the differences that remain after signalling delays and other precticalities have been accounted for.

 

[Grimble]

Inertial units (time and space) are those measured locally (by a local observer within that same frame of reference) in any inertial frame of reference. That they are the same in all inertial frames of reference (Galilean frames) is a demand of the first postulate.

What do you mean by "local"? The "same frame of reference" as what? What you you mean by "in the same frame of reference [...] in any inertial frame of reference"?

I think that what I wrote was quite clear - (by a local observer within THAT same frame of reference)

I was defining what I meant by the terms I used.

By inertial units I mean units within an inertial frame of reference, as measured and referred to within that same frame of reference, in order to avoid anyone claiming that they could be anything else.

By transformed units I mean units that have been transformed by Lorentz transformations.

 

[JesseM]

Let me start by defining the terms I use.
Firstly I do not use the terms primed and unprimed as I have seen these used both ways round and swapped so many times that their use, for me at least, has been compromised;

Inertial units (time and space) are those measured locally (by a local observer within that same frame of reference) in any inertial frame of reference. That they are the same in all inertial frames of reference (Galilean frames) is a demand of the first postulate.

I don't get it. When you say "within the same frame of reference", "same" as what, exactly? And if they are measured relative to a particular frame, then why do you say "they are the same in all inertial frames"?

I think it would help if we dealt with a particular example. Suppose we have two observers, A and B, who are moving inertially relative to one another. Each observer has a ruler at rest relative to themselves, and at each marking on their own ruler there is attached a clock, which is naturally also at rest relative to that observer since the ruler-marking is at rest. Also suppose the different clocks on a given observer's ruler have been synchronized in that observer's frame (because of the relativity of simultaneity, this means each observer will say the clocks on the other observer's ruler are out-of-sync). Each observer uses their own ruler/clock system to make local measurements of the coordinates of events, by looking at which ruler-marking and clock was right next to the event when it happened. For example, if observer A looks through his telescope and sees an explosion happening in the distance, then if he sees the explosion happened right next to the 15-light-second mark on his ruler, and sees that the clock at the 15-light-second mark read 10 seconds at the moment the explosion was happening, then he assigns that event coordinates (x=15 light seconds, t=10 seconds) in his own inertial frame.

If you look at my thread an illustration of relativity with rulers and clocks you can see some diagrams showing two such ruler/clock systems of different observers moving right alongside each other, drawn from the perspective of two different frames. The different frames disagree about which ruler's markings are shrunk and which set of clocks are running slower (and which are synchronized and which are out-of-sync), but they always agree on which readings locally coincide. For example, in the top part of this diagram we see a diagram drawn from the perspective of the A frame, and in the bottom part is a diagram drawn from the perspective of the B frame, although many aspects of the diagrams look different, the circles show that if you pick a particular local event than both frames agree:

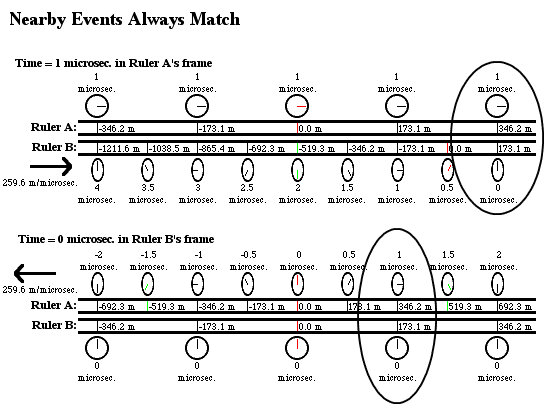
For example, suppose a red firecracker explodes next to the 346.2 meter mark on A's ruler, when A's clock at that mark reads 1 microsecond; then the diagram shows that this firecracker explosion must have also been next to the 173.1 meter mark on B's ruler, when B's clock there read 0 microseconds. Likewise, if you look at some of the earlier diagrams on that thread, you can see that if a blue firecracker exploded next to the 0 meter mark on A's ruler, when A's clock there read 0 microseconds, then the blue firecracker must also have exploded next to the 0 meter mark on B's ruler, when B's clock there read 0 microseconds. No one will disagree about local facts like this.

However, if we ask about the distance and time between the explosion of the blue firecracker and the explosion of the red firecracker, then this is a frame-dependent question. In the A frame the blue firecracker explosion had coordinates (x=0 meters, t=0 microseconds) and the red firecracker explosion had coordinates (x=346.2 meters, t=1 microseconds), so in A's frame the distance between these events was 346.2 meters and the time between them was 1 microsecond. On the other hand, in the B frame the blue firecracker explosion had coordinates (x'=0 meters, t'=0 microseconds) while the red firecracker explosion had coordinates (x'=173.1 meters, t'=0 microseconds), so in B's frame the distance between these events was 173.1 meters and the time between them was 0 microseconds (in B's frame they were simultaneous).

So, would A's measurement of a distance of 346.2 meters and a time of 1 microsecond between the explosions be a measurement in "inertial units" in your terminology? It was after all based on local measurements on A's inertial ruler/clock system. But when B uses his own local measurements on his own inertial ruler/clock system, he gets a different answer for the distance and time between these two explosions (although he does not disagree about which marking and clock-reading on A's system were next to the explosions). Would B's measurement of a distance of 173.1 meters and a time of 0 microseconds also be a measurement in "inertial units"? If so, when you said that inertial units are the same in all inertial frames, what did you mean?

That they are the same in all inertial frames of reference (Galilean frames) is a demand of the first postulate.

The first postulate obviously doesn't demand that the distance and time between a given pair of events be the same when different inertial observers measure it using their own ruler/clock systems. If that's not what you meant, then what are you saying would be the same in all inertial frames of reference?

Transformed units (time and space) are those same inertial units, transformed using the Lorentz equations, which is how they will appear when observed from another inertial frame of reference and are a function of their relative velocity.

Again, can you explain how this terminology applies to my above example? It's true, for example, that if you know that the A frame assigned the red firecracker explosion coordinates (x=346.2 meters, t=1 microsecond), then if you just plug these coordinates into the Lorentz transformation (with gamma = 2 and v = 0.866c), you can deduce that the B frame will assign the red firecracker explosion coordinates (x'=173.1 meters, t'=0 microseconds). Does this make the latter set of coordinates "transformed units", even though they are just what B found using his own inertial ruler/clock system? And note that of course you can also go in reverse--if at first you only know that B assigned the red firecracker explosion coordinates (x'=173.1 meters, t'=0 microseconds), then you can apply the Lorentz transformation to that to deduce that A assigned this same explosion the coordinates (x=346.2 meters, t=1 microsecond). So can every measurement be seen as both inertial units and transformed units, depending on what data you start with and then apply the Lorentz transformation to? If not, then again, please explain the difference between "inertial units" and "transformed units" in terms of the example I have given with the firecrackers and the two inertial ruler/clock systems.

and Galileo and Newton would have agreed that the increased distance traveled by the light would have meant that the speed of light would have increased but the time would have remained constant (relativity principle = 1st postulate)

What does that have to do with the first postulate? The first postulate in no way demands that the time between the events (light hitting bottom mirror) and (light hitting top mirror) be the same in both frames (just like it didn't demand that the time between the blue and red firecracker explosions in my example above should be the same in both frames), if it did then relativity would violate the first postulate. The first postulate just demands that the laws of physics obey the same equations in both frames.

and they would have agreed that the time would have had to increase if the speed were to remain constant (light speed principle = 2nd postulate)

Here you are speculating about what Newton and Galileo would have said about physics that didn't come along until well after they were dead. When I talked about what Newton and Galileo would have said, I didn't mean to talk about what they might have said if they had lived to see new ideas long after their time, I just meant to talk about what is true in classical pre-relativistic physics. In classical physics the 2nd postulate is just false, you can't have any object that has the same speed in all inertial frames.

But Einstein would have said No! We must comply with Both Postulates.

If you are somehow under the impression that the first postulate says different frames should agree on the time and distance between events, and that Einstein says we should comply with that, you are badly misunderstanding the meaning of the first postulate, which again is just about the general equations for the laws of physics, not about the time and distances between a specific pair of events. In fact even in classical physics the distance between a pair of events can be different in two different inertial frames, although in classical physics (unlike in relativity) the time between a pair of events is the same in all inertial frames.

We have the horizontal distance = vT,
The vertical distance h (which, if the clock is ticking seconds in this frame = 1 x c)
and the diagonal distance D, where D = \sqrt{{v^2}{T^2} + {h^2}}

And you quite rightly say that only one frame is needed to reach this point. In fact it could be done using either frame.

Yes, although of course in the rest frame of the clock, v=0 so the path from one mirror to another is purely vertical rather than diagonal in this frame.

Consider, if you will, that if we were to use the light clock's own frame of reference, then we should still say that the observer, traveling at v relative to the clock would still see the diagonal D = \sqrt{{v^2}{T^2} + {h^2}}.

You seem to be confused about what physicists mean when they talk about "using" a given frame of reference--it means that you analyze things using only the distance and time coordinates of that frame (along with coordinate-invariant things like proper times and statements about pairs of events that locally coincide), and don't refer to the coordinates of any other frame. So, it's an incorrect usage of the lingo to say that you can "use the light clock's own frame of reference" to deduce what coordinate distance the light traveled in the observer's frame (though you can use the light clock's frame to figure out what markings and clock readings on the observer's ruler/clock system would line up with the events of the light hitting the bottom and top mirrors).

I have no problem with this at all, nor with the conclusion that:
T is the time for light to travel from the mirror to the observer while
t is the time for the light to travel back to the source
and that if the clock is ticking seconds in its own frame of reference then it will take γ = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} seconds, measured in that same frame, to reach the observer. . . . . . .(1)

Huh? What do you mean when you say "it will take \gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} seconds, measured in that same frame, to reach the observer"? First of all, the time dilation formula t' = t*\sqrt{1 - v^2/c^2} is normally understood purely in terms of relating the time between ticks in the clock's rest frame to the time between ticks in the frame of an observer moving relative to the clock, the idea that it should have something to do with the time for the light of a tick to reach an observer moving relative to the clock as measured in the clock's own rest frame appears to be an idea unique to you. Second, it's not even clear what you mean when you talk about the time for it to reach an observer--won't this be totally dependent on how far the observer is from the clock? If the observer is right next to the source at the bottom mirror at the moment the light has traveled back to the source from the top mirror, then if it takes 1 second for the light to travel from the source to the top mirror and back to the source, that must mean it also takes 1 second for the light to travel from the source to the top mirror and down to the observer in this frame (of course if we knew the time on the observer's clock when the light left the source according to this frame's definition of simultaneity, we could use this frame to calculate the time on the observer's clock when the light returns to the source, and it might be different than 1 second--is this the sort of thing you were getting at?)

But the first postulate also requires that an identical clock, stationary in the observer's frame of reference would also be ticking seconds, identical seconds, as they are both inertial frames of reference, or Galilean frames as Einstein termed them. . . . . . .(2)

What we have to determine here, is how to resolve the difference in what the observer sees, between the 1 second that his own identical clock takes to tick and the γ seconds that he observes the moving clock take for each tick.

Here you seem to be saying that the γ seconds is supposed to be the time in the observer's own frame, but before you said that "if the clock is ticking seconds in its own frame of reference then it will take \gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} seconds, measured in that same frame, to reach the observer". Is γ seconds supposed to be the time between two events in the clock's own frame, or the time between two events in the observer's frame?

Thankfully Einstein gave us the way to resolve the difference in what the observer sees,:
We transform the time observed in the clock's frame using the Lorentz Transformation, and thus we find that T, in transformed units is equal to 1 second inertial time. . . . . . (3)

Please consider that your understanding of SR and what Einstein meant may just be badly confused. Einstein never introduced any distinction between "inertial time" and "transformed time", in SR we just talk about times in different inertial frames, and the Lorentz transformation just distance and time intervals (or distance and time coordinates of individual events) of one inertial frame to the intervals between the same events in a different inertial frame. Also, in SR there is no notion that the first postulate demands that the time and distance intervals between a given pair of events be the same in different inertial frames.

Yes, indeed, one could take the time from any inertial frame (they are all, by definition equal, after all) and transform it (transformed time being that in one frame viewed from another).

The notion of one frame "viewing" another also is not part of SR. Each frame is used to analyze things in terms of the coordinates of that frame alone, and then the Lorentz transformation relates an "analysis-wholly-in-frame-A" to an "analysis-wholly-in-frame-B". For example, in my example above with two firecracker explosions, the wholly-in-frame-A analysis gives the distance between them as 346.2 meters and the time between them as 1 microsecond, while the wholly-in-frame B analysis gives the distance between them as 173.1 meters and the time between them as 0 microseconds. If we start out knowing the wholly-in-frame-A intervals, we can plug them into the Lorentz transformation to deduce the wholly-in-frame-B intervals like so:

gamma*(x - vt) = 2*(346.2 meters - 0.86603c*1 microsecond) = 2*(346.2 meters - (259.63 meters/microsecond)*1 microsecond) = 173.1 meters

gamma*(t - vx/c^2) = 2*(1 microsecond - v*(346.2 meters)/c^2) = 2*(1 microsecond - (259.63 meters/microsecond)*(346.2 meters)/(299.79 meters/microsecond)^2) = 2*(1 microsecond - 1 microsecond) = 0 microseconds

Likewise, if we start out knowing the wholly-in-frame B intervals, we can plug them into the Lorentz transformation to deduce the wholly-in-frame-A intervals:

gamma*(x' + vt') = 2*(173.1 meters - 0.86603c*0 microseconds) = 2*173.1 meters = 346.2 meters

gamma*(t' + vx'/c^2) = 2*(0 microseconds + v*(173.1 meters)/c^2) = 2*(0 microseconds + (259.63 meters/microsecond)*(173.1 meters)/(299.79 meters/microsecond)^2) = 2*(0.5 microseconds) = 1 microseconds

But, in the initial scenario and using only one frame, Ti seconds = γti seconds in time( where γ or \frac{1}{1-\frac{v^2}{c^2}} is the ratio of the distance between the mirrors and that from the mirror to the observer, the diagonal distance)

Again I see no reason why the gamma formula would have anything to do with the "distance to the observer" in the clock's rest frame, you're either confused about what these equations mean in ordinary SR or you're trying to introduce your own novel ideas which are not part of mainstream SR. And the observer's distance from the mirror (which one? Top or bottom?) is constantly changing in this frame, so what moment do you want to talk about the distance from observer to mirror, anyway?

then
{T_t} = \gamma {t_t} seconds in transformed time ...

Again, nothing in mainstream SR corresponds to your distinction between "inertial" time and "transformed" time as far as I can tell, are you trying to introduce new ideas here or are you under the impression that what you are saying is a part of regular SR? Either way you haven't clearly explained what "inertial time" and "transformed time" are supposed to mean, please show how these terms would apply to a specific numerical example like my example with the two firecracker explosions.

 

[JesseM]

(continued from previous post)

I have seen the time dilation formula written (and used) in both forms:

1) {t^'} = t * \gamma

2) {t^'} = \frac{t}{\gamma}

1) is the more commonly used but my research indicates that it is 2) that is the correct one for the following reasons

If different people write it differently it's just because their definition of the primed and unprimed frame is different. If unprimed is the time between a pair of events (like the ticks of a clock) in the frame where those events happen at the same position in space (as would be true in the clock's rest frame if the events represent ticks of a clock), and primed is the time between the same pair of events in a frame moving at speed v relative to the first frame, then the correct formula is 1) above--in the case of clock ticks, the time is greater in the frame where the clock is moving than in the clock's rest frame. On the other hand, if you use primed to be the time in the frame where the events happen at the same position (like the clock's rest frame), and unprimed to represent the time in the frame moving at v relative to the first, then 2) would be the correct formula.

1. It is the one Einstein formulated;
2. It is the one derived from the Lorentz equations;

1. 
   What derivation are you thinking of? Again, it all depends on which frame is supposed to be the one where the events happen at the same position. If we have unprimed be the one where they're at the same position, and we arbitrarily align the origin with the first event so that it has coordinates (x=0, t=0), then the second event must have coordinates of the form (x=0, t=T), where the constant T can have whatever value we choose. Then the Lorentz transformation is:
   
   x' = gamma*(x - vt)
   t' = gamma*(t - vx/c^2)
   
   If we plug (x=0, t=0) into this we get the coordinates of the first event in the primed frame as x'=0, t'=0. Then if we plug (x=0, t=T) in we get:
   
   x' = gamma*(-vT)
   t' = gamma*(T)
   
   So the second event has time coordinate t'=gamma*T in the primed frame, and since the first event had t'=0 in the primed frame, in the primed frame the time interval T' between the two events must be T' = gamma*T, same as your formula 1) above.
   
   On the other hand, if we assume the primed frame was the one where they happened at the same position, then since the primed frame moves at speed v from the perspective of the unprimed frame, in time T the clock will have moved a distance vT, so if the first tick happened at (x=0, t=0), the second must have happened at (x=vT, t=T). The first event again must have coordinates (x'=0, t'=0) in the primed frame when we use the Lorentz transformation. But the second event will have:
   
   x' = gamma*(vT - vT) = 0
   t' = gamma*(T - v^2*T/c^2) = gamma*T*(1 - v^2/c^2) = T*(1 - v^2/c^2)/sqrt(1 - v^2/c^2) = T*sqrt(1 - v^2/c^2) = T/gamma.
   
   So, in the primed frame the time interval T' between the two events must be T' = T/gamma in this case. Again, it's just a matter of whether you want primed or unprimed to be the frame where the events happened at the same position, once you have established that convention, there is no question about what the time dilation formula is supposed to look like.
   

   [*]A http://www.answers.com/topic/special-relativity#Time_dilation_and_length_contraction" reverses the terms and thereby reverses the derived formula;

   How does it reverse the terms? If follows the more common convention where unprimed is the rest frame of the clock, and therefore derives your formula 1), T' = gamma*T.
   

   [*]Einstein himself, proved
   "[URL="[PLAIN]http://www.bartleby.com/173/11.html"[/URL] that {x} = c{t} and that {x^'} = c{t^'} so the formulae for Length contraction and time dilation have to be analagous or these two equations cannot both be correct;

   He did not show that x = ct and x'=ct' are general relations which hold for events of arbitrary coordinates, this was just supposed to be the equation of motion for a light beam which was released from the x=0 at t=0 (which also is assumed to coincide with x'=0 and t'=0 in the primed frame in the Lorentz transformation). It's easy to show using the Lorentz transformation that if you pick an event on the worldline of this light beam which occurs at coordinates x=cT and t=T in the unprimed frame (which satisfies x = ct), then in the primed frame this same event has coordinates:
   
   x' = gamma*(x - vt) = gamma*(cT - vT) = gamma*T*(c - v) = c*gamma*T*(1 - v/c)
   t' = gamma*(t - vx/c^2) = gamma*(T - vcT/c^2) = gamma*T*(1 - v/c)
   
   So, you can see from this that is true that this event must have coordinates which satisfy x'=c*t' in the primed frame.
   
   And I already showed that both version 1) and version 2) of the time dilation formula can be derived from the Lorentz transformation depending on which frame you want the clock to be at rest in, so you can see that both formulas must be equally compatible with the equation of motion for the light beam, since they were all derived from the same Lorentz transformation equations.
   

   [*]Minkowski space time shews quite conclusively exactly how length contraction and time dilation are, in fact, the same process and could, incidentally, have been termed 'length dilation' and 'time contraction' and all those terms would have been correct! (I will shew this later).

   Time dilation and length contraction are conceptually different things when illustrated on a Minkowski diagram--time dilation deals with the time between a single pair of events in two different frames, while length contraction does not deal with the distance between a single events in two different frames, rather it deals with the distance between two parallel worldlines at a single moment in two different frames (with 'at a single moment' depending on each frame's definition of simultaneity). It would be possible to come up with a spatial analogue for time dilation which deals with the distance between a single pair of events, in which case the equation would look just like the time dilation equation, and likewise to come up with a temporal analogue for length contraction which deals with the time between two parallel spacelike surfaces at a single position in two different frames, in which case the equation would look just like the length contraction equation. If you're interested you can take a look at the diagram I drew which neopolitan posted in post #5 of this thread, where we were discussing the issue of whether it's meaningful to talk about "time contraction" or "length dilation" (I don't really recommend reading the whole thread though, it went on a lot of tangents).
   

   But no it doesn't, just because someone at sometime in the distant past decided to use the labels length-contraction and time-dilation implying one increases while the other decreases people have been making the mistake of thinking the formulae are opposites, while they are in fact analagous.

   Do you agree that if \Delta t represents the time between ticks of a clock in the clock's rest frame, and \Delta t' represents the time between ticks in a frame moving at speed v relative to the clock, then the correct formula is \Delta t' = \gamma * \Delta t? And do you agree that if L represents the distance between either end of an object in the object's rest frame, and L' represents the distance between either end of that object in a frame moving at speed v relative to the object (with the positions of each end measured simultaneously in whatever frame is measuring the distance), then the correct formula is L' = \frac{L}{\gamma}?
   

   from which we can see that if c = \frac{L}{t} then c = \frac{L^'}{t^'} which of course it has to do.

   Nope, you cannot show that the speed of light is the same in two frames using only length contraction and time dilation, you have to take into account the relativity of simultaneity too.
   

   Nope, the fact that the speed of light is c in both frames cannot be derived from the length contraction and time dilation formulas alone, you also have to take into account the relativity of simultaneity. See my post here for a numerical example of how to take into account all three factors to show that two frames will both measure a light beam to move at c.

   Yet Einstein did it directly from the Lorentz transformation formula, very simply. It isn't complicated. See paragraph 6

   Obviously you can derive the fact that a light beam moves at c in all frames using the Lorentz transformation, since the Lorentz transformation was itself derived using the second postulate and since time dilation, length contraction and the relativity of simultaneity can all be derived from it too. But we were talking about your claim (which you repeat above) that somehow one could combine the length contraction equation and the time dilation equation alone to get the invariance of c, without making use of the full Lorentz transformation equations, and also without making use of the relativity of simultaneity. It's this claim which doesn't make any sense (on the other hand, if you use the time dilation equation along with what I called the 'spatial analogue of time dilation', which unlike length contraction deals with the distance between a single pair of events, then you can combine these two equations to get the conclusion that distance/time for two events on the worldline of a lightbeam must always equal c).

 

[Rasalhague]

I think that what I wrote was quite clear - (by a local observer within THAT same frame of reference)

By local do you mean that the measurements are to be made at all relevant points in spacetime so that there are no delays to take into account between an event and it being recorded? If so, why do you emphasise "within that same frame"? Are you aware that if an observer is present at an event according to one frame, then all frames will agree on the observer being present at that event?

I was defining what I meant by the terms I used.

By inertial units I mean units within an inertial frame of reference, as measured and referred to within that same frame of reference, in order to avoid anyone claiming that they could be anything else.

By transformed units I mean units that have been transformed by Lorentz transformations.

...these transformed values being intervals of time and space in some other inertial frame, hence my suggestion that terms such as "input" and "output" might be less confusing, or untransformed and transformed, or something like that.

and Galileo and Newton would have agreed that the increased distance traveled by the light would have meant that the speed of light would have increased but the time would have remained constant (relativity principle = 1st postulate) and they would have agreed that the time would have had to increase if the speed were to remain constant (light speed principle = 2nd postulate)
But Einstein would have said No! We must comply with Both Postulates.

The idea of the time dilation derivation from the example of the light clock is that, since the speed of light is the same in both frames, a greater time must elapse between "ticks" in the frame where the light clock is moving than elapses between ticks in the frame where the light clock is at rest.

And you quite rightly say that only one frame is needed to reach this point. In fact it could be done using either frame.

In the light clock's rest frame, v = 0, so D = h. The formula is still meaningful, but it doesn't serve its intended purpose of demonstrating how the size of an interval of time between a given pair of events depends on which reference frame they're referred to.

Have a look at the section called Time distortion here which begins "Consider the situation shown in figure f." I often find it helps to read different authors' explanations of the same idea.

http://www.lightandmatter.com/html_books/0sn/ch07/ch07.html

1) is the more commonly used but my research indicates that it is 2) that is the correct one for the following reasons:

I don't think it's a matter of one being correct and the other incorrect. It just depends what you need to calculate and what you're using the prime symbol to represent.

 

[Grimble]

I don't get it. When you say "within the same frame of reference", "same" as what, exactly? And if they are measured relative to a particular frame, then why do you say "they are the same in all inertial frames"?.

Before I say anything else will somebody, anybody, please read what I have written?


I DID NOT write "within the same frame of reference" I wrote "within that same frame of reference" - bold used for emphasis!

Which if read as written changes the meaning somwhat.

PS. I apologise Jesse (if I may call you that?) but yours is the second of two replies that have made the same misquote of what I had written...

 

[Grimble]

Huh? What do you mean when you say "it will take \gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} seconds, measured in that same frame, to reach the observer"? First of all, the time dilation formula t' = t*\sqrt{1 - v^2/c^2} is normally understood purely in terms of relating the time between ticks in the clock's rest frame to the time between ticks in the frame of an observer moving relative to the clock, the idea that it should have something to do with the time for the light of a tick to reach an observer moving relative to the clock as measured in the clock's own rest frame appears to be an idea unique to you.

If the clock's time is one second, the height is ct where t=1, the horizontal distance is vt' and the diagonal distance is ct', where t' is the time for the light to reach the observer who passed the clock at the start of the 'tick' all measured in the clock's frame, then {t^'}= \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} by the application of simple old Pythagoras.

 

[JesseM]

Before I say anything else will somebody, anybody, please read what I have written?


I DID NOT write "within the same frame of reference" I wrote "within that same frame of reference" - bold used for emphasis!

Which if read as written changes the meaning somwhat.

I don't see how it changes the meaning. I repeat the question, with that word changed:

Inertial units (time and space) are those measured locally (by a local observer within that same frame of reference) in any inertial frame of reference. That they are the same in all inertial frames of reference (Galilean frames) is a demand of the first postulate.

I don't get it. When you say "within that same frame of reference", "same" as what, exactly? And if they are measured relative to a particular frame, then why do you say "they are the same in all inertial frames"?

PS. I apologise Jesse (if I may call you that?) but yours is the second of two replies that have made the same misquote of what I had written...

No problem, and sorry for misquoting (and yeah, feel free to just call me Jesse), but as I said I don't understand why "the same" vs. "that same" makes a difference in how I should interpret your statement. Again, "same" as what?

 

[Grimble]

Please accept my apologies for the state of this thread, good people, it is so easy to be diverted by arguments of minutiae.

Let me say that I have come to SR on my own using the Einstein paper that I quote from.

I found that to be clear, concise and easy to understand.

I then looked further, on the web, principally in Wikipedia etc. and was intersted to find things that did not match what I had learned from Einstein.

I do not pretend (honestly) to know the answers, but for me, just being told 'thats the way it is' doesn't satisfy, I like to know WHY and HOW.

One of the major problems I find is the constant pulling apart every statement I make and telling me to rephrase it or disecting what the words mean!

I have been told (not just in this thread) that proper time is the term to use and that there is no such thing as proper time...

that there is no need to use A' and B', but that A & B will do: then I am told that I should use A' and B'...

having experienced so much criticism for using the wron terms, I tried defining my own - inertial and transformed units, and earning immediate criticism despite attempting to define exactly what I meant by the use of those terms.

No matter how I try and ask questions or address the points that don't seem to add up for me all I get is constant critical disection of the language I am trying to use.

And it is not just that I am unused to the particular terms you use, but you can't even agree amongst yourselves about the use of the terms.

Top this with a tendency to read into what I am saying, what you expect me to be saying, without bothering, it seems, to actually reading it, and the whole exercise becomes frustrating.

One thing which I find particularly annoying (and which I am sure will annoy anyone who experiences it) is to be told what I am thinking, when what I am told is not, and sometimes is the very opposite, of what I am thinking.

Moaning over!

My background is scientific, I studied physics at university, many years ago, followed by 25 years in computing, where I spent many years solving problems, designing systems and in support work, where the prime skill was to be able to take written documents, designs, and complete software systems and find the bugs in them.

I have come to you for assistance in understanding SR and answering questions that arise where the modern understanding seems to fit uneasily with what Einstein wrote.

So I ask for your patience and your help

Thank you, Grimble

 

[JesseM]

Huh? What do you mean when you say "it will take \gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} seconds, measured in that same frame, to reach the observer"? First of all, the time dilation formula t' = t*\sqrt{1 - v^2/c^2} is normally understood purely in terms of relating the time between ticks in the clock's rest frame to the time between ticks in the frame of an observer moving relative to the clock, the idea that it should have something to do with the time for the light of a tick to reach an observer moving relative to the clock as measured in the clock's own rest frame appears to be an idea unique to you.

If the clock's time is one second, the height is ct where t=1, the horizontal distance is vt' and the diagonal distance is ct', where t' is the time for the light to reach the observer who passed the clock at the start of the 'tick' all measured in the clock's frame, then {t^'}= \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} by the application of simple old Pythagoras.

But to say the observer "passed the clock at the start of the tick" is too vague, this only works if you specifically assume the observer was passing the top mirror at the moment the light was departing from the bottom of the clock; the time to reach the observer would be zero if the observer was passing the bottom at the moment light was departing from there, and somewhere in between zero and the time you give if he was passing the middle. And even if we add in the qualification that you are talking about the time for light from the bottom to reach the observer who passes the top at the moment the light was emitted, I don't really see the point of this calculation--the time for the light from the bottom of the clock to reach the observer has nothing to do with the time the observer will judge for the light clock to make one tick in his own rest frame, and thus nothing to do with the time dilation equation (you could after all place the observer in a completely different position than next to the top mirror when light is emitted from the bottom, in which case the time for the light from the bottom to reach him would be different, but it wouldn't change his judgement about the time of one tick of that light clock in his own frame).

 

[JesseM]

I have been told (not just in this thread) that proper time is the term to use and that there is no such thing as proper time...

Who has told you "there is no such thing as proper time"? It is a very basic idea in relativity, so either you misunderstood what the person was saying, or they are in error.

that there is no need to use A' and B', but that A & B will do: then I am told that I should use A' and B'...

Who said it makes any difference what notation you use for the two frames? All that really matters is that you distinguish them, and explain clearly what each frame is in physical terms (for example, in the time dilation equation it is important to clearly state which of the two frames is the rest frame of the clock whose ticks are being measured, this is usually labeled as the unprimed frame but as long as you clearly explain which frame it is when you write the time dilation equation you are free to use a different notation).

having experienced so much criticism for using the wron terms, I tried defining my own - inertial and transformed units, and earning immediate criticism despite attempting to define exactly what I meant by the use of those terms.

I did not think your explanation of what you meant by these terms was at all clear, but I didn't just criticize, I also asked you to elaborate how the terms would apply to some specific numerical example, in hopes of clarifying.

No matter how I try and ask questions or address the points that don't seem to add up for me all I get is constant critical disection of the language I am trying to use.

Sorry if it seems like you are getting too much criticism, but as I said I've also been asking for clarifications. When discussing a technical subject like relativity, there's no getting around the need for precision in one's use of language but I think this sort of back-and-forth can help make sure we all have a clear idea of what the terms mean, and pinpoint ambiguities that need to be addressed.

One thing which I find particularly annoying (and which I am sure will annoy anyone who experiences it) is to be told what I am thinking, when what I am told is not, and sometimes is the very opposite, of what I am thinking.

I hope I have not "told you what you are thinking", but if the meaning of your words is unclear to me, I think it is helpful to say in my own words what I think you might be saying, so you can respond and tell me something like "yes, that is what I meant" or "no, that's a misunderstanding, let me rephrase". This is all part of the back-and-forth I was talking about...if you didn't know how your words were being interpreted by me, how would we ever figure out if we were on the same page with the meaning of various words and phrases or if we were totally talking past each other?

 

[Rasalhague]

Let me say that I have come to SR on my own using the Einstein paper that I quote from.

I found that to be clear, concise and easy to understand.

Hi Grimble, I don't mean to be snide, but I think you should seriously consider the possibility, if JesseM's explanations seem to you to conflict with this book, that there are flaws in your understanding of what Einstein meant. I know it can be frustrating to think you've got it at last only to be told that you're mistaken. But learning has its ups and downs, and these ideas are notoriously counterintuitive. I'm sure you'd rather know the truth than settle for a superficial feeling of being right.

I then looked further, on the web, principally in Wikipedia etc. and was intersted to find things that did not match what I had learned from Einstein.

Wikipedia can be confusing, especially when a lot of people have worked on one article, and it isn't always right. After all, anyone can contribute to it. If you're trying to learn something new, it can be hard to know how reliable a Wikipedia article is, and the same goes for websites generally. Might I recomment the Relativity chapter in Benjamin Crowel's online physics textbook Simple Nature?

http://www.lightandmatter.com/

A more detailed introduction to special relativity that I've found very useful is Spacetime Physics by Taylor and Wheeler (which isn't online as far as I know). John Baez recommends it in his Guide to Relativity Books.

http://math.ucr.edu/home/baez/physics/Administrivia/rel_booklist.html

I find it helps to read about a difficult topic in a few different textbooks because one often sheds light on aspects of the topic that are unclear in another. Reading different presentations of the same material can also alert me to mistaken ideas I may have formed. Apparent contradictions can sometimes show me that I didn't understand something as well as I thought I did.

I do not pretend (honestly) to know the answers, but for me, just being told 'thats the way it is' doesn't satisfy, I like to know WHY and HOW.

Of course.

One thing which I find particularly annoying (and which I am sure will annoy anyone who experiences it) is to be told what I am thinking,

Sorry if I've added to that frustration by anything I've written! Sometimes I may have said what I thought you meant or suggested possible meanings, but that's only so that you know what meaning I've got from your words, so that you can set me straight if I've misunderstood you.

One of the major problems I find is the constant pulling apart every statement I make and telling me to rephrase it or disecting what the words mean!

Often rephrasing something that people haven't understood can make it clearer. The subject we're talking about involves aspects of reality that are so alien to our everyday experience that we can't rely on our intuition but need to be very careful about our language. Many expressions that make perfect sense in ordinary contexts are imprecise when we're talking about relativity.

 

[JesseM]

Wikipedia can be confusing, especially when a lot of people have worked on one article, and it isn't always right. After all, anyone can contribute to it. If you're trying to learn something new, it can be hard to know how reliable a Wikipedia article is, and the same goes for websites generally. Might I recomment the Relativity chapter in Benjamin Crowel's online physics textbook Simple Nature?

http://www.lightandmatter.com/

A more detailed introduction to special relativity that I've found very useful is Spacetime Physics by Taylor and Wheeler (which isn't online as far as I know). John Baez recommends it in his Guide to Relativity Books.

http://math.ucr.edu/home/baez/physics/Administrivia/rel_booklist.html

Here's another good online intro to SR, written in a Q&A format:

http://www.oberlin.edu/physics/dstyer/Einstein/SRBook.pdf

 

[Grimble]

Hi Grimble, I don't mean to be snide, but I think you should seriously consider the possibility, if JesseM's explanations seem to you to conflict with this book, that there are flaws in your understanding of what Einstein meant. I know it can be frustrating to think you've got it at last only to be told that you're mistaken. But learning has its ups and downs, and these ideas are notoriously counterintuitive. I'm sure you'd rather know the truth than settle for a superficial feeling of being right.

Hello Rasalhague, thank you and I don't think that you are in any way being snide. Your contributions have always been received as couteous and well considered.

Please accept that I agree with your sentiments above! I am quite willing to accept that there may be flaws in my understanding - the possibility of me being right and everyone else wrong is, frankly, not something I would put money on

No, when I say that when I find conflicts, I am trying to convey that the fact that I find conflicts, is something that I need to resolve; my constant carping and saying "but that's wrong" is no help whatsoever! it just encourages the different sides to dig their heels in and pull their hair!

I apologise for this. I should be asking questions not making contraversial statements.

And I am quite happy if someone says "were you thinking ... "
or "it seems to me that what you are saying is ..."
or just to rephrase one of my comments...
That is what would be referred to as "testing understanding" and is a valuable tool in communication...
No, the annoying thing is for someone to say "I know what you are thinking..."
And then go on to restate something far from what I meant or something that I have no problem with.

I am grateful for the time you all spend trying to help an old man.

I will keep at it for I know it will all fit into place, all neat and tidy. It has to for all science is logical, it has to be, that is how it works, we just have to find and understand the right logic.

Your humble student Grimble

 

[JM]

I know that this is a very basic question but what is the correct formula for time dilation?:

The correct formula is the one corresponding to the calculation that you intend to make.
Consider the Lorentz transformations in the form:
x = m ( X - vT), ct = m ( cT - vX/c ),
where m is the term Einstein named 'gamma', y,z = Y,Z = 0, and k( x,t ) is the coordinate frame whose origin moves in the positive direction along the X axis of K( X, T). For the following calculations v = 0.8c, so m = 10/6.
1. Suppose you take Ks point of view ( take K to be at rest) and consider points lying along the line X = vT. Enter this espression in the right side of the transforms to get t = T/m, i.e. t is less than T. Einstein presented this case in his 1905 paper.
2.Take ks viewpoint and consider points along the line x = - vt. Enter this on the left to obtain T = t/m, i.e. t is greater than T.
3. Take ks view and consider points at x = 0 and various values of t. Enter these values on the left and get X = vT, and get T = mt, i.e. T is greater than t. This is the case Einstein presents in the book you cited.
4. Take Ks view and consider points on the line X = 0.5 cT. From the transforms T =t, and x = - X.
From the above we can see that t can be less than, equal to, or greater than T. A single term, such as 'dilation' seems inadequate to describe these varied calculations.

I hope this helps.
JM

 

[Rasalhague]

The angle LaTeX Code: \\beta represents the speed of either frame relative to the other, as a fraction of the speed of light: v/c.

Correction: the angle I labelled beta in these diagrams should have been labelled arctan beta!