Abhijeet Verma
- 8
- 0
Since the latex is not appearing, I request you to please click https://brilliant.org/discussions/thread/time-period-of-vertical-circular-motion/ , to view with complete formatting.
Please help.
Thanks.
P.S-This is not schoolwork or homework.
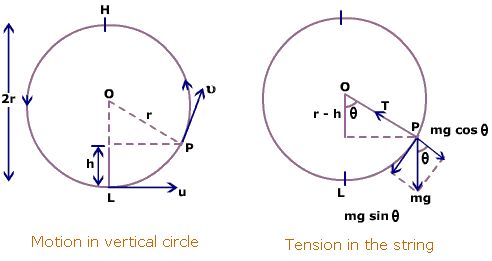
Note: \(x\) has been used for the angle with the vertical, measured in anticlockwise direction.
As shown in the figure, the tangential acceleration \({ a }_{ t }\) is \(gsinx\) .
Thus, the angular acceleration will be \(\frac { { a }_{ t } }{ R }\) , where \(R\) is the radius of the circle.
Writing
\[\frac { \omega d\omega }{ dx} =-\frac { gsinx }{ R }
int\]
\[\int _{ \frac { v }{ R } }^{ \omega }{ \omega d\omega } =\frac { g\int _{ 0 }^{ x }{ sinxdx } }{ R } \\ { This\quad gives\\ \omega =\sqrt { \frac { 2g(1-cosx) }{ R } +{ \frac { v }{ R } }^{ 2 } } =\frac { dx }{ dt } }\]
Now, I don't know how to integrate this expression between \(0\quad to\quad 2\pi \), to calculate the time taken for complete oscillation.
So, plese help by proceeding from here or if there is any other method to calculate the time period, please mention.
Thanks.
Please help.
Thanks.
P.S-This is not schoolwork or homework.

Note: \(x\) has been used for the angle with the vertical, measured in anticlockwise direction.
As shown in the figure, the tangential acceleration \({ a }_{ t }\) is \(gsinx\) .
Thus, the angular acceleration will be \(\frac { { a }_{ t } }{ R }\) , where \(R\) is the radius of the circle.
Writing
\[\frac { \omega d\omega }{ dx} =-\frac { gsinx }{ R }
int\]
\[\int _{ \frac { v }{ R } }^{ \omega }{ \omega d\omega } =\frac { g\int _{ 0 }^{ x }{ sinxdx } }{ R } \\ { This\quad gives\\ \omega =\sqrt { \frac { 2g(1-cosx) }{ R } +{ \frac { v }{ R } }^{ 2 } } =\frac { dx }{ dt } }\]
Now, I don't know how to integrate this expression between \(0\quad to\quad 2\pi \), to calculate the time taken for complete oscillation.
So, plese help by proceeding from here or if there is any other method to calculate the time period, please mention.
Thanks.