Torque or the moment of a force

[Fightfish]

torque or the "moment" of a force

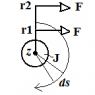
Found myself thinking these few days about torque or the "moment" of a force. It seems to occur as common sense based on everyday experience, but I just cannot seem to figure out why a force acting on the object further away from the pivot as compared to one nearer to the pivot would generate a greater moment and angular acceleration of the body about the pivot. Apologies upfront if this is trivial, but this has really got me stumped =(

 

[Bob S]

Think of a seesaw (lever arm) with unequal masses and unequal lever arms on each side.

M₁L₁ = M₂L₂ for balance (equal torque)

Bob S

 

[Fightfish]

Think of a seesaw (lever arm) with unequal masses and unequal lever arms on each side.

M₁L₁ = M₂L₂ for balance (equal torque)

Bob S

Well, that doesn't really help in understanding why a mass further away has a larger "torque per unit mass". In any case, this classic lever arm thing led me to D'Alembert's principle and virtual work, and I guess they do somewhat explain the phenomenon.

 

[Lsos]

It's hard to explain "why"...it's simply the way the world works. To get a feel for it, try to undo a bolt with a wrench. You'll notice that the longer the wrench, the easier it is to undo the bolt...because the torque applied to it is greater.

 

[Bob S]

It's hard to explain "why"...it's simply the way the world works. To get a feel for it, try to undo a bolt with a wrench. You'll notice that the longer the wrench, the easier it is to undo the bolt...because the torque applied to it is greater.

The torque (Newton-meters) is the same with a longer wrench, but the force (Newtons) is less.
Bob S

 

[think001]

If you think about the example given by a previous poster, in which you try to undo a bolt with a wrench, of course you will notice that it is easier to turn the wrench when you hold the part of the handle that is furthest away from the bolt. The force required to turn the wrench is directly related to the distance from the pivot point.

This is just circular motion and work. (F=mv^2/r - As r increases, the force required to move an object around a pivot point decreases, but since w=Fs, the increase in r resulting in a direct decrease in F means that the amount of energy needed, to move the handle of the wrench from point A to point B, will be less and is the reason that it feels 'easier' to turn. The torque (=Fd) remains the same because the decrease in F is balance by the increase in d. Drawing a diagram helps to make sense of it..)

It's also the same reason the gears on a bicycle work the way they do.

Hope this helps..

 

[Hootenanny]

Welcome to Physics Forums think001.

This is just circular motion and work. (F=mv^2/r - As r increases, the force required to move an object around a pivot point decreases

This equation represents the radial force (experienced by an object moving under circular motion), rather than the tangential force required to turn the wrench.

Whilst the qualitative results remain unchanged (one creates a greater torque when applying the same force at a greater distance from the pivot), one should keep in mind that the quoted equation is not applicable in this case.

 

[think001]

Thanks for the welcome and reply Hootenanny - I will rethink the situation keeping what you said in mind. :)

 

[dE_logics]

It's a law...a law is something which is opensource yet you can't question it...it's forbidden. :PTorque and moment are a measure of rotation in a sense that they have the ability to figure out what effects will the force have on the specific arrangement; it might happen that 2 forces (A and B) which are actually twice to that of a single force (C) where A, B are in the same directions and C in the opposite are not able to overcome the torque produced by C...as a result the arrangement moves in the direction of C.

But if we rearrange the location of A and B, it can produce massive torque such that it easily overcomes C...thus the force alone in rotation is not a factor determining the net direction of rotation; this is where torque comes in...using it you can predict in which direction will the arrangement move.

 

[SystemTheory]

The sketch shows flywheel mass with constant moment of inertia J computed about the axis of rotation z (into the sketch), such as the central axis of a uniform solid cylinder. Define the torque as T = F x r, the cross product of the force vector in the x-y plane and the radius of action. For a 90 degree angle T = Fr.

To find the rate of acceleration apply Newton's Second Law in rotational analog form:

T = J \alpha

\alpha = \frac{T}{J} = \frac{Fr}{J}

So when F/J is constant an increase in radius r generates an increase in angular acceleration alpha about the axis of rotation. Note also the force traces a longer path s and does more work per revolution, which must increase the kinetic energy more per revolution for a longer radius. The work is Fds which is geometrically equal to T d-theta. You must take an integral to find the work done through an arc length s. When force is constant you can find the work using the geometry of an angle and its arc W = Fs.

 

[DocZaius]

As r increases, the force required to move an object around a pivot point decreases, but since w=Fs, the increase in r resulting in a direct decrease in F means that the amount of energy needed, to move the handle of the wrench from point A to point B, will be less and is the reason that it feels 'easier' to turn.

My understanding of the situation was that the amount of energy needed to move the handle of the wrench from point A to point B will not be less but be just as much as if one moved it from a shorter radius. Even though you apply less force when at a greater radius from the axis, you apply that force over a longer distance. The reason it feels easier isn't because less energy was expanded but because it is easier for us humans to spread the force over longer intervals.

Is my understanding incorrect?

 

[SystemTheory]

It depends on what you hold constant.

The OP asks why the same force causes greater angular acceleration at a greater radius, if I understand the original question. So my assumption is the force stays constant and the radius increases.

If you want to keep the torque constant, a greater radius requires less force to produce the same torque (and the same rate of acceleration for a body of constant moment of inertia J).

The work depends again on what is being held constant and what is allowed to vary.

 

[DocZaius]

What I am saying is that for a wrench to have gotten from point A to point B, the energy expanded will always be the same, and doesn't depend, as think001 says, on how far from the axis the force was applied. Force and radius might be variable, but the energy cannot be "saved." You could have torqued the wrench from point A to point B with a small force and a large radius or with a large force and a small radius, but either way you used just as much energy. Right?

 

[SystemTheory]

The work done by a torque acting through an angle theta:

Work = \int T(\theta) d\theta

The integral accumulates the area under a curve if torque is a variable.

By going from A to B, I assume you mean a constant displacement angle at a different radius? If so, the work is constant if you adjust the force and radius to hold the torque constant.

 

[DocZaius]

Right, it is as I thought. There is no energy saved from applying the same torque with a greater radius (and thus lesser force) throughout the same displacement angle.