Alex126
- 84
- 5
I have a general understanding of how torque works, at least for "simple" objects that can be drawn as a single "bar" under the effect of various forces. In this problem there is a slightly more "complex" object though, and I'd like to know if there is a way to solve it without doing what I did to come to a solution, i.e. a way to solve it considering the object as a whole, and not by arbitrarily considering only a part of it (which feels like fair game, but maybe it's not...?).
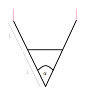
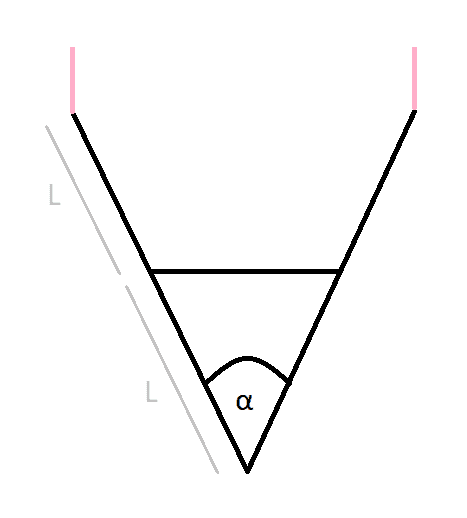
A ladder is hanging upside down from a ceiling, and it's attached to the ceiling with two ropes. The ladder is made of two "legs" and it also has a horizontal piece in-between the legs which provides some force R; the horizontal piece has negligible mass. Each "leg" is long 2L, and each "leg" weighs a known force W (120 N). The angle α between the two legs, at the point where they meet, is known (60°).
Determine the force R.
Drawing (provided by the textbook):
At the point of equilibrium:
ΣForces = 0
ΣTorque = 0
Torque = F⊥ * d (with d = distance between fulcrum and point where the force is applied, and F⊥ being the component of the force that is perpendicular to the object)
OR
Torque = d * F * sin (θ) (with θ being the angle between the vectors d and F)
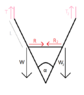
This would be my free body diagram attempt:
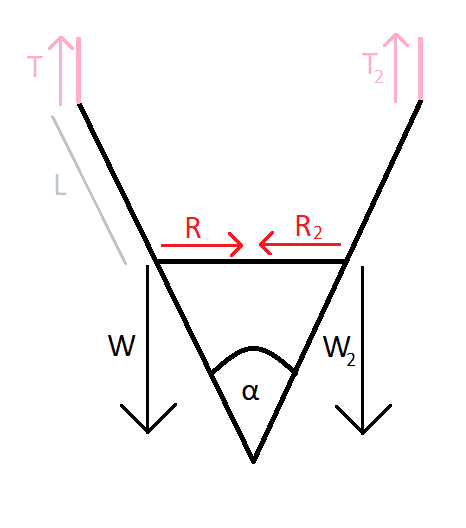
I'm not sure what the middle bar of the ladder was supposed to do, so R could point inwards or outwards depending on whether it prevents the "legs" from splitting apart or joining together. I assumed it pointed inwards.
As anticipated though, I couldn't really set the exercise up this way.
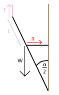
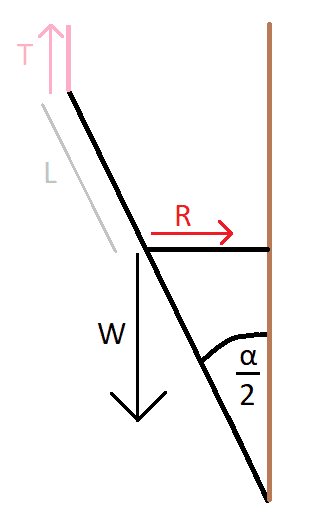
What I did instead was this: I cut the object in half, since it's basically a symmetrical situation where we get the same things on the left and right side. At that point, I considered the left leg alone, and imposed the conditions for equilibrium. It looked like this:
Then I chose a fulcrum at the top of the "leg". With that fulcrum:
Torque from T = 0 (distance = 0)
Torque from R = R*cos (α/2) * L
Torque from W = W*sin (α/2) * L
With that fulcrum, R would produce a counterclockwise rotation, and W would produce a clockwise rotation. So the sum of the torques becomes:
R*cos (α/2) * L - W*sin (α/2) * L = 0
So R = W*tan (α/2)
This gives the correct result of 69 N.
-------
Once again though, I want to know if it's possible to solve the problem without having to resort to splitting it in half, i.e. by using the full picture instead.
I tried doing that, putting the fulcrum in the same spot, and up to the point where I calculate the torque for the left leg it all went well. Then I tried to figure the distance d to use in the torque formulas for the right half, and realized I have no idea what to use for distance.
So, how can I handle this object, which does not have the typical "straight bar" appearance, and make the torque formulas work for it?
I tried by placing the fulcrum at the bottom point of the ladder, where the two legs meet, but then I end up with an equation that has the same left and right terms. So I tried moving the fulcrum to another point, the middle of the left leg, and reached the point where I'm stuck because I don't know what to use for d in the torque for W2, R2, and T2.
So...how would you have set the problem, if splitting the object in half was not an option?
Homework Statement
A ladder is hanging upside down from a ceiling, and it's attached to the ceiling with two ropes. The ladder is made of two "legs" and it also has a horizontal piece in-between the legs which provides some force R; the horizontal piece has negligible mass. Each "leg" is long 2L, and each "leg" weighs a known force W (120 N). The angle α between the two legs, at the point where they meet, is known (60°).
Determine the force R.
Drawing (provided by the textbook):
Homework Equations
At the point of equilibrium:
ΣForces = 0
ΣTorque = 0
Torque = F⊥ * d (with d = distance between fulcrum and point where the force is applied, and F⊥ being the component of the force that is perpendicular to the object)
OR
Torque = d * F * sin (θ) (with θ being the angle between the vectors d and F)
The Attempt at a Solution
This would be my free body diagram attempt:
I'm not sure what the middle bar of the ladder was supposed to do, so R could point inwards or outwards depending on whether it prevents the "legs" from splitting apart or joining together. I assumed it pointed inwards.
As anticipated though, I couldn't really set the exercise up this way.
What I did instead was this: I cut the object in half, since it's basically a symmetrical situation where we get the same things on the left and right side. At that point, I considered the left leg alone, and imposed the conditions for equilibrium. It looked like this:
Then I chose a fulcrum at the top of the "leg". With that fulcrum:
Torque from T = 0 (distance = 0)
Torque from R = R*cos (α/2) * L
Torque from W = W*sin (α/2) * L
With that fulcrum, R would produce a counterclockwise rotation, and W would produce a clockwise rotation. So the sum of the torques becomes:
R*cos (α/2) * L - W*sin (α/2) * L = 0
So R = W*tan (α/2)
This gives the correct result of 69 N.
-------
Once again though, I want to know if it's possible to solve the problem without having to resort to splitting it in half, i.e. by using the full picture instead.
I tried doing that, putting the fulcrum in the same spot, and up to the point where I calculate the torque for the left leg it all went well. Then I tried to figure the distance d to use in the torque formulas for the right half, and realized I have no idea what to use for distance.
So, how can I handle this object, which does not have the typical "straight bar" appearance, and make the torque formulas work for it?
I tried by placing the fulcrum at the bottom point of the ladder, where the two legs meet, but then I end up with an equation that has the same left and right terms. So I tried moving the fulcrum to another point, the middle of the left leg, and reached the point where I'm stuck because I don't know what to use for d in the torque for W2, R2, and T2.
So...how would you have set the problem, if splitting the object in half was not an option?