SUMMARY
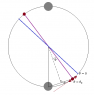
The discussion focuses on the mathematical analysis of the Cavendish experiment, specifically deriving the gravitational constant G and examining the harmonic nature of oscillations in a torsion pendulum setup. The expression for G is established as G = 2π²Lr²θ/(MT²). For part c, participants explore whether the oscillation of the small balls is harmonic and derive the period of oscillation, ultimately leading to the conclusion that the period T can be expressed as T = 2π√(mL²r₀)/(2κ(r₀ - Lθ₀cosθ₀)). The importance of correctly interpreting the distance r in relation to the angle θ is emphasized throughout the discussion.
PREREQUISITES
- Understanding of torsion pendulum mechanics
- Familiarity with gravitational force equations
- Knowledge of differential equations and simple harmonic motion
- Ability to apply the binomial approximation in physics
NEXT STEPS
- Study the derivation of gravitational constant G in various experimental setups
- Learn about the mathematical modeling of simple harmonic motion
- Explore the application of the binomial approximation in physics problems
- Investigate the principles of torsion pendulum dynamics and their applications
USEFUL FOR
Physics students, educators, and researchers interested in gravitational experiments, torsion pendulum dynamics, and the mathematical foundations of oscillatory motion.