Torsional Vibration Natural Frequency & Nodal Position

[SeaMist]

Hi

I was doing an exercise of calculating the "natural frequency" of a 3-mass system. The problem is like:

A shaft has three inertia on it of 6, 4 and 10 kgm2, respectively viewed from left to right. The shaft connecting the first two is 2.6 m long with a stiffness of 12 x 106 Nm/radians and the shaft connecting the last two masses has the length of 2 m and a stiffness of 10 x 106 Nm/radians. The system is supported in bearings at both ends. Ignore the inertia of the shafts and find;
a. The natural vibration frequencies of the system;
b. Locations of the nodes by using a graphical method;

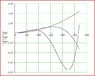
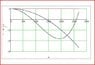
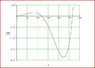
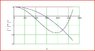
I have calculated the natural frequency of the system and the nodal position alright, but I have difficulty conceptualising/ understanding the "Physical Meaning" of the graphs that I have obtained.

I would alsp appreciate if some one can help me understanding the physical meaning of the graphs attached, and also any interpretation of the graphs.

Thanks
SeaMist

 

[FredGarvin]

The first plot looks like mode shapes. However, without units or descriptions on either plot, it's tough to say what you have. The second looks like some kind of displacement plot. Did you normalize it by chance?

 

[SeaMist]

Comments

Apologies for the late post, got stuck up with some asignments. I am posting the solution graphs for the problem described in the original post.

The units are;
Omega (greek) = rads/sec
Torq = Nm
Angles (alpha, beta, gamma) = rads

What can we interpret from the graphs that we have obtained from the solution?

Would much appreciate the comments and point.

Thanx

 

[SeaMist]

forgot to attach the graph that deterimes the nodes.