- #1
emr13
- 33
- 0
1. The base of the yellow triangle has length 8 inches; its height is 10 inches. Each of the circles is tangent to each edge and each other circle that it touches. There are infinitely many circles. The radius of the largest of them is __________ and the total area of all the circles is ___________.
There's a picture with the largest circle centered at the base of the triangle, and continously smaller circles until the peak of the triangle.
n/a
I figured out the radius of the largets circle by using this equation:
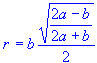
and got 2.708131846.
The problem I'm having is determining the correct infinite series to figure out the area of all the triangles. I know the area of each circle is pi*r^2, but the radius of each circle is dependent on the sides of the triangle, which change for each circle.
There's a picture with the largest circle centered at the base of the triangle, and continously smaller circles until the peak of the triangle.
Homework Equations
n/a
The Attempt at a Solution
I figured out the radius of the largets circle by using this equation:
and got 2.708131846.
The problem I'm having is determining the correct infinite series to figure out the area of all the triangles. I know the area of each circle is pi*r^2, but the radius of each circle is dependent on the sides of the triangle, which change for each circle.