Transform impedance of given network

[magnifik]

I'm having trouble finding the impedance of the simple given network below:

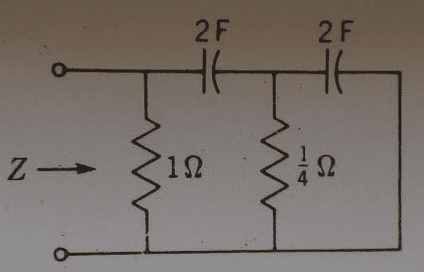
I know Z(s) of each capacitor is 1/2s, but I'm confused on what's in series/parallel.
How can you tell? I know it has to do with the nodes. Any help would be appreciated.

 

[gneill]

Components are in parallel when their leads share exactly two nodes. That means they will always share the same potential difference across them.

Components are in series when the same current flows through all of them (no branching!).

 

[magnifik]

i attempted to do (1/4 || 1/2s) + 1 + 1/2s and am getting (s^2 + 3s + 1)/(s(s+2)), but this is the incorrect answer :\ what am i doing wrong here?

 

[gneill]

i attempted to do (1/4 || 1/2s) + 1 + 1/2s and am getting (s^2 + 3s + 1)/(s(s+2)), but this is the incorrect answer :\ what am i doing wrong here?

The 1 Ohm resistor is not in series with the others. This should be clear by the fact that it parallels the input!

You've got the 1/4 Ω resistor in parallel with the final 2F capacitor. This is correct. That net impedance in in series with the middle 2F capacitor, as you've calculated. But the final 1Ω resistor is NOT in series with the result.

If it's confusing, redraw your circuit after each simplification, replacing the simplified bits with a single generic impedance icon (say a rectangle to represent it).

 

[magnifik]

ok, thank you!

(1/4 || 1/2s)
= (1/4)(1/2s) / (1/4 + 1/2s)
= 1/(2s + 4)

1/(2s + 4) + 1/2s
= (s+1)/(s^2+2 s)

(s+1)/(s^2+2 s) || 1
= (s+1)/(s^2+3 s+1)