This really cleared things up for me. I never thought to see the angular momentum that way. Here is my current standing:
Mechanical energy is collectively conserved. I can make equation number one that includes linear and rotational energy. Am I wrong on this as well? Can linear and rotation energy be conserved separately like we do with momentum?
Linear momentum is conserved independently. I can make equation number two that only includes linear momentum.
Angular momentum is conserved independently. I can make equation number three that only includes angular momentum.
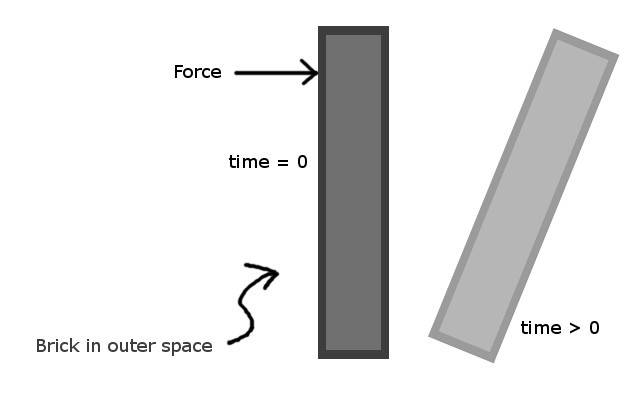
However, I understand that one object can have two forms of angular momentum. It can have angular momentum about its own CM and angular momentum about the system CM. This means that there are two additional variables to worry about: There is the ball angular momentum around the system CM. There is the brick angular momentum around the system CM (after the impact). So I have five variables: ball linear, ball system-angular, brick linear, brick self-angular, and brick system-angular. But I have only three equations/constraints. No worries!
kuruman said:
The fancy system-CM angular momentum can be related to the cross product of linear momentum and position from the system CM. I can apply that constraint to the ball. And I can apply that constraint to the brick.
Now my degrees of freedom equals my number of constraints! That is a good deal. (5 = 5)
So I believe everything I just said is just another way to look everything I've been taught on this thread.
Now, I'll throw a wrench into the mix. I want the ball to be a small block. Let's call it the block-brick system. The small-block makes the impact off-center from its own CM. This means we have yet another variable: The small-block gains self-angular momentum after the impact.
Here is the only way I can think to solve this:
Take angular energy to be conserved independently.
Take linear energy to be conserved independently.
That way, I can split equation number one into two energy equations. I don't know if that is physically accurate though. I'll have six equations and six variables for the block-brick system. If you haven't already guessed, I'm trying to understand how to write an algorithm for
general simulation of elastic collisions.
Again, I really applicate all the help. This kind of discussion is invaluable to me.
I attempted to quote that equation from kuruman exactly but it was giving me trouble with the special characters.