- #1
annamal
- 381
- 33
Below is a pulley with mass and a string around it where the tension of one end of the string is 20 N and the tension of the other end of the string is 60 N. I know there is a net torque due to the differing tensions of the string, so I am wondering what the translational forces are on the pulley. We have a force B of the screw holding the pulley up against the weight of the pulley Mg. So would the translational force in the y direction of the pulley be
-20 - 60 - Mg + B = 0?
If so, I am wondering how to translationally (not rotationally) take into account forces on other points of the pulley like at point P. For example, due to the tension in the string around the pulley, there is a 20 N force in the ##-\vec i + -\vec j## direction and a 60 N force in the ##\vec i + \vec j## direction. Is that correct? Because it seems like I am adding extra force on the pulley.
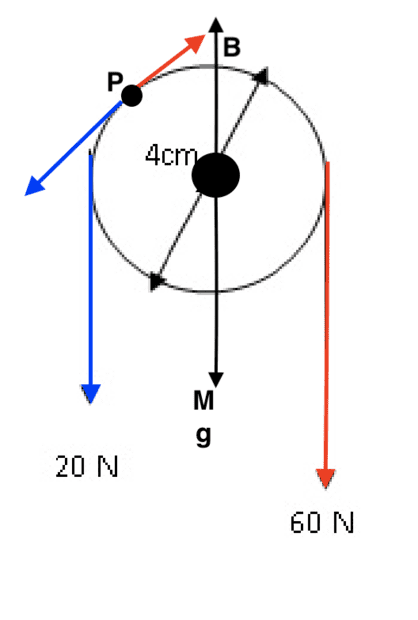
-20 - 60 - Mg + B = 0?
If so, I am wondering how to translationally (not rotationally) take into account forces on other points of the pulley like at point P. For example, due to the tension in the string around the pulley, there is a 20 N force in the ##-\vec i + -\vec j## direction and a 60 N force in the ##\vec i + \vec j## direction. Is that correct? Because it seems like I am adding extra force on the pulley.