Transmission line transient simulation

[isison]

Dear all,

I am simulation a lossy transmission line like this:
http://www.ece.uci.edu/docs/hspice/hspice_2001_2-2878.jpg

with G having zero conductance (open). So it is a standard lossy transmission line with RLC components. All R, L, and C values are the same, so there is no variation from segment to segment. There are total 1000 segments being simulated in HSPICE.

The input function is a step function that goes from low to high at t=0. I look at the propagation of this signal through the transmission line at a certain time. I obtained a voltage vs. position plot like this:

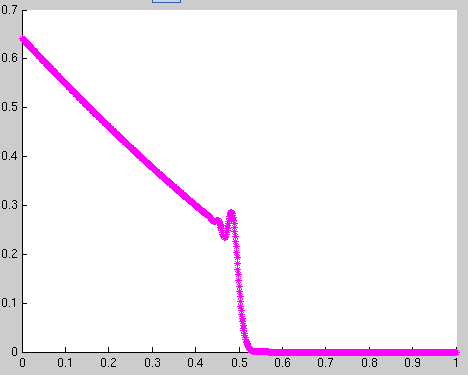
The x-axis is the position, and y-axis is the voltage sampled at each segment.

The general shape of this transient curve makes sense to me. It is step function signal front propagates toward right. However, there is this oscillation at the signal front that I seen unable to get rid of.

What is the physical reason behind this oscillation? It's best if you can explain this in a layman term to someone who is not familiar with transmission line analysis.

Thanks!

 

[phyzguy]

I think it is an oscillation of the lumped L and C components you used in your simulation. To test this, the frequency of the oscillation should be $\omega = \frac{1}{\sqrt{}L C}$. In the real transmission line, the L and C elements are continuous distributed elements, not lumped, discrete elements. You could make the simulation more realistic by increasing the number of L and C elements and decreasing their size. For example, if you had 2000 elements, each with L/2 and C/2, the frequency of this oscillation would be twice as high. As you pass to the continuum limit, with the number of elements going to infinity and the size of each element going to zero, this oscillation will disappear.

 

[manzana]

I think phyzguy is probably right. But I don't understand your graph. Are we looking at a single point on the line as the pulse goes by? Then why is it a falling edge? Are we just scanning down the line after the pulse settled out? Remember that we will get a + reflection off the end of the line, too. Try simply hooking up a dc source and wait for everything to settle out and tell us what you see.

 

[phyzguy]

No, the OP said we are looking at all of the points on the line at a given time. So the X-axis is position. So the signal hasn't reached the points with x>0.5 yet.

 

[manzana]

Oh, that is really pretty neat! I am used to looking at a point while time marches on. Since Hspice never lies (ahem) this is of course correct. You are seeing how mother nature propagates the signal down the line. If it wasn't for the little LC's you would just have a voltage divider with a zero prop time. That little oscillation is your friend! It brings you your cable TV.