SUMMARY
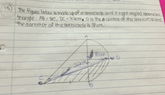
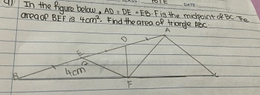
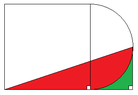
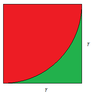
The discussion focuses on calculating the area of a triangle and a semi-circle. Participants confirm that if the base and height of two triangles are equal, their areas are also equal. The main calculation involves determining the area of a large triangle using the formula A_T = 1/2 * base * height and subtracting the area of a semi-circle segment from a square to find the remaining area. The final area calculation is presented as A = (r^2)(1/2 + π/4) with r specified as 9 cm, leading to A = (81/4)(2 + π) cm².
PREREQUISITES
- Understanding of triangle area calculations
- Knowledge of semi-circle area and arc properties
- Familiarity with algebraic manipulation of area formulas
- Basic geometry concepts related to shapes and their dimensions
NEXT STEPS
- Study the derivation of triangle area formulas
- Learn about the properties of semi-circles and their areas
- Explore advanced geometric problem-solving techniques
- Investigate applications of π in area calculations
USEFUL FOR
Students, educators, and math enthusiasts seeking to deepen their understanding of geometric area calculations and problem-solving strategies involving triangles and circles.