Trigonometric Equations Problems - Rather Confused

[AN630078]

Homework Statement

Trigonometric equations are by far one of my weakest areas. I have been practising to improve and refine my understanding but I am still a little uncertain in areas. I have attempted some questions below but was wondering if anyone could offer me some advice on how to improve my workings or apply more suitable methods.

Question 1; Solve the following equations giving your solutions as exact fractions of π in the range 0 ≤θ ≤2 π:

a. sin θ=√3/2
b.cos2θ=0.5
c.tan (2θ-π/4)=1

Question 2; Sketch the graphs y=2cos x and y=tan x.
a. How many values of x satisfy the equation in the range 0 ≤θ ≤360 degrees?
b. Show that the x-values at the points of intersection satisfy the equation 2sin^2x+sins-2=0
c. Solve the equation 2cos x=tan x between 0 and 360 degrees

Relevant Equations

tan x=sin x / cos x
sin^2x+cos^2x=1

Question 1;
a. sin θ=√3/2
θ=arcsin √3/2
θ=π/3 rad
sin √3/2=60 degrees
60 degrees *π/180=π/3 rad.

To find the other solutions in the range, sin θ=sin(π-θ)
π-π/3=2π/3
The solutions are π/3 and 2π/3 in the range 0 ≤θ ≤2 π

b. cos2θ=0.5
2θ=arccos 0.5
2θ=π/3 rad
Divide both sides by 2;
θ=π/6 rad

To find the other solutions in the range, cos θ=cos(2π-θ)
2π-π/3=5π/3
Divide by 2 =5π/6

The solutions are π/6 and 5π/6 in the range 0 ≤θ ≤2 π

c. tan (2θ-π/4)=1
2θ-π/4=arctan 1
2θ-π/4 = π/4
Add π/4 to both sides;
2θ=π/4+π/4
2θ=π/2
Divide both sides by 2:
θ=π/4

To find other solutions in the range add π/2:
π/4+π/2=3π/4
3π/4+π/2=5π/4
5π/4+π/2=7π/4

The solutions are π/4, 3π/4, 5π/4 and 7π/4 in the range 0 ≤θ ≤2 π

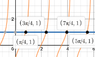
I have also attached what I think the graphs of these equations would look like to find the required solutions. How can I improve or broaden my answers to more extensively exhibit my workings. I am a little confused here admittedly.

Question 2;
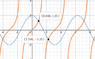
a. I have just plotted the graph using desmos and attached an image here. Clearly, there are two values of x that satisfy the equation in the range. Do I need to add anything to this statement, I feel the response is a little brief for the question?

b. Using the trigonometric identities;
tan x=sin x / cos x
and sin^2x+cos^2x=1

2cos x=tan x
Multiply the whole equation by cos x:
2cos x=sinx
Using the identity sin^2x+cos^2x=1, 2cos x becomes: 2(1-sin^2x)
2(1-sin^2x)=sinx
Expand the brackets;
2-2sin^2x=sinx
Subtract sin x from both sides;
2-2sin^2x-sinx=0
Divide by -1;
2sin^2x+sinx-2=0

c. To solve the equation 2cos x=tan x
This is shown to be equal to the quadratic;
2sin^2x+sinx-2=0

Let sin x = u
2u^2+u-2=0

Using the quadratic formula; a=2, b=1, c=-2
u=-b±√b^2-4ac/2a
u=-1±√1^2-4*2*(-2)/2*2
u=-1±√17/4
u=0.780 and x=-1.28 to 3.s.f

sin x = -1±√17/4
x=arcsin 0.78 =51.3 degrees to 3.s.f
x= arcsin -1.28 = no real solutions as x cannot be smaller than 1 for real solutions

To find other solutions in the range 0 ≤θ ≤360 degrees use sin θ=sin(180-θ):
180-51.3=128.7 degrees

So the solutions are 51.3 and 129 degrees to 3.s.f?

Would this be correct. I am very uncertain of trigonometric equation problems and I have been teaching myself which is perhaps why my knowledge is a little unstable and I am am sure in places erroneous. I would be very grateful of any help

 

[Mark44]

Your post is quite long, with two questions with three parts each. Few members will want to wade through all of your work and comment on it.

I am closing this thread. Please repost questions 1 and 2 in separate threads. In the future, please limit your posts to one question with up to three parts.