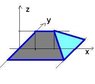
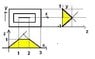
The first thing you should do is draw a graph. Because it is difficult to draw in three dimensions, I prefer to draw xy, xz, and yz graphs. Here, none of the equations involve both x and y so you really only need xz and yz graphs.
x- z= 0 is the z= x line, of course, and x+ z= 3 is the line z= 3- x that has x intercept (0, 3) and z intercept (3, 0). Draw those two lines on the xz-graph.
y+ z= 1 is the line z= 1- y with y intercept (1, 0) and z intercept (0, 1). z= y+ 1 has y intercept (-1, 0) and z intercept (0, 1). Draw those two lines.
Now, imagine turning the yz graph so its z axis corresponds to the z axis on the xz graph. That will give you some idea of what the figure looks like. Now, looking at that, there is nothing bounding the region between z= 1- y and z= y+ 1 in the y-direction. Adding the "z= 0" condition we do have a bounded region below the z= 1- y plane but then the z= y+ 1 plane plays no part. The only bounded region I see here lies within the triangle bounded by z= x, z= 3- x, and z= 0 below the plane z= y+ 1.
I see that, for that region, x lies between 0 and 1. For each x, z lies below the two lines x- z= 0 and x+ z= 3. I think, then that we will need to break this into two integrals, the first for x= 0 to the x-coordinate of the point of intersection, the second for x= that value to 3.