Troubleshooting nuclear decay, electron binding energies, internal contributions

[Graham87]

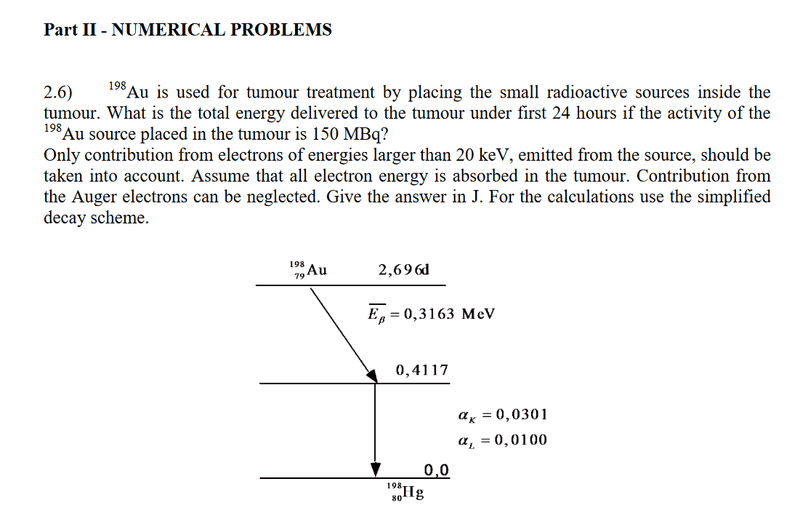
Homework Statement

See pic

Relevant Equations

See pic

How do you know which binding energy shell to use? In the solution it uses K and L2. Why specifically L2 and not L3 or L1 for example?

And what should I do with the information to omit electrons lower than 20kev? I initially thought that meant to omit the electron binding energies lower than 20kev. But L2 which is lower than 20kev is included, so which expression represents electron energy? If it is ΔE - B(L) then shouldn’t L3 be included since it also has a higher energy than 20kev?

 

[TSny]

My guess is that there are some typos as indicated below:

The $L_1$ should be $K$ and the $L_2$'s should just be $L$. This corresponds with the given binding energies:

Perhaps the value $B(L)_{Hg} = 14.2087$ keV is a weighted average over the $L_1$, $L_2$, and $L_3$ levels.

I'm not sure about the 20 keV restriction. Since $\overline E_\beta$, $B(K)_{Hg}$ and $B(L)_{Hg}$ are all in the hundreds of keV, there doesn't appear to be any need to worry about requiring the electrons to have an energy greater than 20 keV.