LCSphysicist
- 644
- 162
- Homework Statement
- The problem is how to get a equation of a position of a body that suffer a impulse and now is on a orbit that oscillate. The conditions are:
The body was in a circular orbit at initial.
L remains constant
The circular orbit is stable
The energy increases a little.
The force is such that it has all the necessary conditions above, and, obviously, are central attractive and varies with the distance.
- Relevant Equations
- E = T + U'
L = mwr^2
Initial radius is ro
f = -kr^n
First of all, i know that the motion will be bounded, is not necessary to know if the motion will be closed or not.
Second, by analyzing the graphic of a effective potential with such conditions, the motion will agree with harmonic motion.
Ok
I don't know how to prove the harmonic oscillation, here i want help.
But, just assuming that it is true, the general equation is
r = M + acos + bsin
Since w = (√(k/m)), and k is the second derivation of the potential energy [here i use the effective potential instead just the potential] in the ro initial.
All of this bring to the final equation:
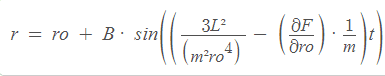 [Actually the terms between parentheses of the sin is under root , i forget write this.]
[Actually the terms between parentheses of the sin is under root , i forget write this.]
I don't know to take off t.
And How to determinate B
Second, by analyzing the graphic of a effective potential with such conditions, the motion will agree with harmonic motion.
Ok
I don't know how to prove the harmonic oscillation, here i want help.
But, just assuming that it is true, the general equation is
r = M + acos + bsin
Since w = (√(k/m)), and k is the second derivation of the potential energy [here i use the effective potential instead just the potential] in the ro initial.
All of this bring to the final equation:
I don't know to take off t.
And How to determinate B