Trying to verify these work relations

[creative9k]

I need to verify these three work relations and don't know where to even start.

Wtotal= ΔK, Wc= -ΔU and Wnc = ΔE


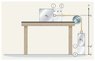
The details for the whole problem were A block of mass m1 = 2.40 kg is connected to a second block of mass m2 = 1.80 kg, as shown in the figure. The two masses start from rest and are moving with a speed of 2.05 m/s just before m2 hits the floor.

I already figured out the answers to the first three parts of the questions and the answers were.

d=0.937m
Wc=16.5J
Wnc=-7.72J

Honestly I'm not sure what they are even looking for as means for an answer.

 

[tal444]

It would help if you could give us a diagram.

 

[creative9k]

It would help if you could give us a diagram.

I apologize, I knew I forgot something.