Two Blocks and a Pulley with Friction

[. Arctic.]

Homework Statement

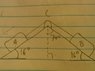
Blocks A and B are connected by a cable that passes over support C. Friction between the blocks and the inclined surfaces may be neglected. Knowing that motion of block B up the incline is impending when m_B = 4.5 kg, determine:

(a) the coefficient of static friction between the rope and the support
(b) the largest value of m_B for which equilibrium is maintained

Homework Equations

T₂ = T₁e^(μ_sβ) (1)
β is in angle in radians
W = mg

The Attempt at a Solution

My problem is that for part (b), my answer is wrong. I would like to know where I went wrong in my calculations. Thanks for the help in advance.

I found the forces working on Block A
ƩF_x = 0
→ T_A - W_Asin(16) = 0
T_A = 24.336 N

Then, Block B
ƩF_x = 0
→ W_Bsin(16) - T_B = 0
T_B = 12.168 N

Then, I looked at support C where I found the angle to be 32°, and I used (1) to find the static friction.
β = (32)(∏/180) ≈ 0.559
T_A = T_Be^(μ_sβ)
24.336 N = (12.168 N)e^(μ_sβ)
e^(μ_sβ) = (24.336 N)/(12.168 N)
μ_sβ = ln [(24.336 N)/(12.168 N)]
μ_s = (1/0.559)*ln [(24.336 N)/(12.168 N)]
μ_s ≈ 1.240

Then, since I know T_B has to be greater than itself to upset the equilibrium, I did

T_B = T_Ae^(μ_sβ)
T_B = (24.336 N)e^[(1.240)(0.559)]
T_B ≈ 48.673 N

Then, to get the mass I divided the T_B by g = 9.81

m_B = (48.673)/(9.81) ≈ 4.962 kg

That is wrong.

 

[haruspex]

Then, to get the mass I divided the T_B by g = 9.81
m_B = (48.673)/(9.81) ≈ 4.962 kg

You forgot that the mass isn't hanging straight down.

 

[. Arctic.]

I just tried multiplying it by sin(16), which of course didn't work, but dividing by it sure did work. Thanks.