jeff12
- 40
- 2
Homework Statement
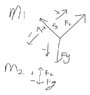
A block of mass m1 = 3.70 kg on a frictionless inclined plane of angle 30.0° is connected by a cord over a massless, frictionless pulley to a second block of mass m2= 2.30 kg hanging vertically. What are (a) the magnitude of the acceleration of each block and (b) the direction of the acceleration of m2? (c) What is the tension in the cord?
Homework Equations
F=ma
The Attempt at a Solution
I set the coordinate system according to the diagram above.
System: m1
Ft+Fg=m1a
Ft-m1gsinθ=m1a
System: m2
Ft+Fg=m2a
Ft-m2g=m2a
Ft=m2g+m2a
Then I plug in both of them.
m2g+m2a+m1gsinθ=m1a
m2a-m1a=-m1gsinθ-m2g
Then I sub in the values
a=3.15?
I don't know what I did wrong. The correct answer is 0.735.