Two cylinders rotating with contact at an angle (reformulation of the problem)

[wrobel]

Some time ago there was a problem with the following picture somewhere out here. I think this problem was underestimated a little bit.

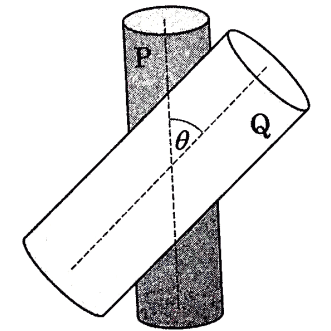
Let us reformulate the problem. Assume that each cylinder, if it was not influenced by the other one, could rotate freely about its fixed axis. But the cylinders press each other with a force $N>0$. The coefficient of dry friction between them is $k>0$. Assume also that both cylinders experience torques $\tau_P,\tau_Q$. The torques are constants and directed along the corresponding axes of cylinders. Moments of inertia $J_P,J_Q$ of cylinders are given.
The task is to draw a phase diagramme on the plane $\omega_P,\omega_Q$ for different values of parameters. Here $\omega_P,\omega_Q$ are the angular velocities. I even think that it would be interesting for an educational journal. I think to give it to my students.

Any comments are welcome :)

 

[anuttarasammyak]

In the case of $\theta=\pi/2$ torque of P and Q push each other to move along the axis. Do you allow such translation motion to P and Q ?

 

[wrobel]

no, I consider the motion along the axis to be forbidden for both cylinders

 

[anuttarasammyak]

So we allow the rolls slip in that case. In general we allow slip of the axis component of roll velocity v sin$\theta$.

 

[wrobel]

So we allow the rolls slip in that case.

yes and they are slipping for any nonzero angular velocities; $\theta\in(0,\pi/2]$

 

[etotheipi]

@wrobel I'd be interested to see how you went about solving this. I haven't gotten very far

Draw a Cartesian frame $O\mathrm{xyz}$ with $O$ at the point of contact of the cylinders, the $\mathrm{y}$ axis parallel to the axis of $P$ and the $\mathrm{z}$ axis pointing vertically upward. Let the unit vectors parallel to the axes of each cylinder be $\mathbf{e}_P := \mathbf{e}_y$ and $\mathbf{e}_Q := \mathbf{e}_y \cos{\theta} + \mathbf{e}_x\sin{\theta}$. Writing $\boldsymbol{\omega}_P = \omega_P \mathbf{e}_P$ and $\boldsymbol{\omega}_Q = \omega_Q \mathbf{e}_Q$ the relative velocity of the cylinders at the point of contact is $$\boldsymbol{V} := \boldsymbol{v}_P(O,t) - \boldsymbol{v}_Q(O,t) = (r_p \boldsymbol{\omega}_P + r_Q \boldsymbol{\omega}_Q) \times \mathbf{e}_z = \mathbf{e}_x(r_P \omega_P + r_Q \omega_Q \cos{\theta}) - \mathbf{e}_y r_Q \omega_Q \sin{\theta} $$Now define $\hat{\boldsymbol{V}} := \boldsymbol{V} / |\mathbf{V}|$. The friction force acting on $P$ due to $Q$ is $\mathbf{F}_P = - k N \hat{\boldsymbol{V}} = - \mathbf{F}_Q$. Let $\mathcal{A}_P$ and $\mathcal{A}_Q$ be arbitrary points along the axes of $P$ and $Q$ respectively. The moment $\Gamma_P$ associated with $\mathbf{F}_P$ about the axis $(\mathcal{A}_P, \mathbf{e}_y)$ of $P$ is$$\Gamma_P = r_P \mathbf{e}_z \times (- k N \hat{\boldsymbol{V}}) \cdot \mathbf{e}_y = \frac{-r_P k N(r_P \omega_P + r_Q \omega_Q \cos{\theta})}{|\boldsymbol{V}|}$$Similarly, the moment $\Gamma_Q$ associated with $\mathbf{F}_Q$ about the axis $(\mathcal{A}_Q, \mathbf{e}_Q)$ of $Q$ is $$\begin{align*}

\Gamma_Q &= -r_Q \mathbf{e}_z \times (k N \hat{\boldsymbol{V}}) \cdot (\mathbf{e}_y \cos{\theta} + \mathbf{e}_x\sin{\theta}) \\ \\

&= \frac{-r_Q k N([r_p \omega_p + r_Q \omega_Q \cos{\theta}]\cos{\theta} + r_Q \omega_Q \sin^2{\theta})}{|\boldsymbol{V}|} = \frac{-r_Q k N(r_p \omega_p \cos{\theta} + r_Q \omega_Q )}{|\boldsymbol{V}|}

\end{align*}$$The system of differential equations to solve is$$\begin{bmatrix} \dot{\omega}_P \\ \dot{\omega}_Q \end{bmatrix} = \begin{bmatrix} \frac{1}{J_P} (\tau_P + \Gamma_P) \\ \frac{1}{J_Q} (\tau_Q + \Gamma_Q) \end{bmatrix}$$and it looks like it is a bit difficult to solve

 

[wrobel]

Qualitative analysis of ODE is needed I guess