- #1
dmcoleman
- 1
- 0
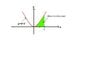
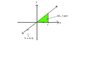
Hi I have been thinking about an idea I have involving calculus that I think someone here can help me with. Is there a way you can determine a simple function (like f(x)=Ax) that has the same area dA from X to dX as another complicated function like f(x)=x^2. If you refer to the two attachments to this post you will see two graphs of two functions f(x)=X^2 and f(x)=Ax. The area under the curve of both functions from x=0 to x=2 are equal. My question is how can we determine the value of the variable A in the function f(x)=Ax if these conditions are to be satisfied. Thanks.