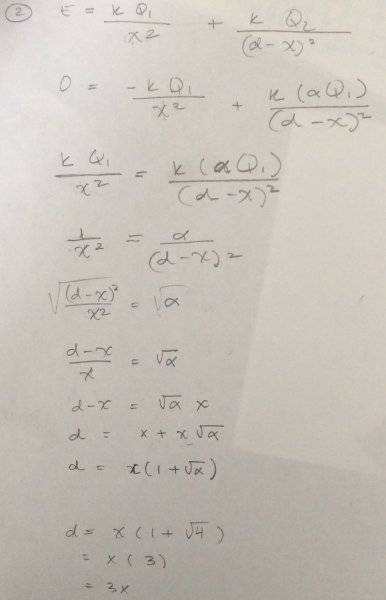SUMMARY
The discussion focuses on determining the position where the electric field is zero between two positive point charges, Q1 and Q2, separated by a distance d. The user is tasked with finding a general expression for this position, defining Q2 as alphaQ1, where alpha is greater than zero and not equal to one. The conversation highlights the importance of correctly accounting for the direction of electric fields generated by positive charges and emphasizes the need for clarity in mathematical expressions, particularly regarding the introduction of negative signs in calculations.
PREREQUISITES
- Understanding of electric fields generated by point charges
- Familiarity with algebraic manipulation of equations
- Knowledge of the concept of superposition in electrostatics
- Basic grasp of the relationship between charge, distance, and electric field strength
NEXT STEPS
- Explore the concept of electric field superposition in detail
- Study the derivation of electric field equations for multiple point charges
- Learn about the implications of charge polarity on electric field direction
- Investigate the effects of varying charge magnitudes on electric field distributions
USEFUL FOR
Students of physics, particularly those studying electrostatics, as well as educators seeking to clarify concepts related to electric fields and charge interactions.
 This is what I have, but unsure about it
This is what I have, but unsure about it