Two slit diffraction and energy conservation

[LmdL]

Hi all,
I have a small misunderstanding about the energy conservation in diffraction from 2 slits.
First, I understand the energy conservation of interference from 2 slits.
If intensity from each slit is I, then I have intensity of 2I after slits plane.
Interference is given by:

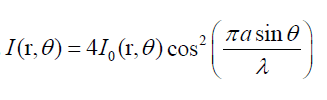
So at bright fringes I get cos^2=1, so intensity is 4I. And in dark fringes I get cos^2=0, so intensity is 0.
Since interference just distributes the intensity over screen, the cos^2 pattern with 4I maximum and 0 minimum, on average, results in a 2I intensity, as just after the slits plane.
Now I add the diffraction, i.e. multiply by sinc^2. This leads to a lower intensity pattern compared to the case of pure interference, so averaged intensity will be lower then 2I. Where the energy is lost?

 

[Simon Bridge]

You are comparing averages between two different situations... no special reason the averages have to be the same.
Instead, compare the incoming energy with that leaving the slits.

 

[blue_leaf77]

Where the energy is lost?

The fields in the slit plane and in the observation plane is connected through Fourier transform in the case of far-field diffraction, therefore you don't need to worry about energy conservation because it is guaranteed by Parseval's theorem
$$
\int |E(x)|^2 dx = \int |\tilde{E}(x')|^2 dx'
$$
where $\tilde{E}(x') = FT[E(x)]$, $x$ is coordinate in the slit plane, and $x'$ the coordinate in the observation plane.

 

[LmdL]

Still didn't get it. I understand that this must be true (energy is conserved) and even understand why it's true (intuitive) for the interference case. But when the diffraction is introduced, I cannot get it in intuitive way. The only explanation I can think of is that I don't multiply by sinc^2 in the diffraction case, but rather by Asinc^2, where A is some normalization constant which ensures energy conservation. So the overall picture will look like that:

And not like that: