Two tanks are connected by a valve and line

[joejoe121]

Homework Statement

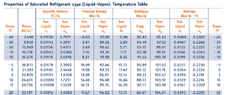
Two tanks are connected by a valve and line. The volumes are both 1 cubic meter with R-134a at 20 C, quality 15% in tank A and tank b is evacuated. The valve is opened and saturated vapor flows from A into B until the pressures become equal. The process occurs slowly enough that all temperatures stay at 20 C during the process.
a) Initial specific internal energy in A is......kj/kg
b) Initial mass in A is.......kg
c) Final specific internal energy of R-134 is..........kj/kg
d) Total work during process is.......kj
e) Total heat transfer during the process is.......kg

Relevant Equations

u = u_f + x(u_g-u_f)
v= = v_f +x(v_g-v_f)
mass = V/specific volume

I've attached all my work and data table I used to answer the questions but there isn't an answer key so I would like a second opinion.

 

[Chestermiller]

In parts c, d, and e, the total mass is constant. This tells you the mass fraction vapor in the final state (assuming equal final mass in the two tanks).

 

[joejoe121]

In parts c, d, and e, the total mass is constant. This tells you the mass fraction vapor in the final state (assuming equal final mass in the two tanks).

I'm sorry, I don't follow.

 

[Chestermiller]

The total final mass in each tank is half the initial mass in the first tank. You know the final temperature, pressure, and volume of each tank, so this tells you the final quality. Once you know this information, you can calculate the final internal energy in each tank.

 

[joejoe121]

The total final mass in each tank is half the initial mass in the first tank. You know the final temperature, pressure, and volume of each tank, so this tells you the final quality. Once you know this information, you can calculate the final internal energy in each tank.

I found my internal energy for Tank B by finding my values at state 2.
u = u_f + x(u_g - u_f)
but I need x so I solve quality in state 2 by using saturated volume values at 20 F and solved for specific volume by using V2 = V_a + V_b = 2 meter cubed. I used the mass of the initial tank and since mass is constant, I used it with specific volume = 2m^3/m.
Next, I plugged in my quality, and values given at 20 F for saturated vapor and liquid to get the specific internal energy at 20F using the final quality.
Lastly, I used Q = m(u_2 - u1) u_2 being the specific internal energy I solved for in the previous step and u_1 is from Part a.

I hope my writing gets my point across concisely.