Two unknown charges accelerating an object

[Ozmahn]

Homework Statement

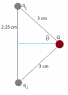
Two point charges q1 and q2 are held in place 4.50 cm apart. Another point charge -2.00μC of mass 6.00g is initially located 3.00 cm from each of these charges and released from rest. You observe that the initial acceleration of -2.00μC is 354m/s^2 upward, parallel to the line connecting the two point charges. Find q1 and q2.

Homework Equations

$F=ma$
$F= kQq1/r^2$

The Attempt at a Solution

I drew a sketch of the problem, with q1 directly above q2 (.045m away). The first thing I did was find the total force by plugging in the mass and acceleration:

$F = (0.006kg)*(354m/s^2) = 2.124 N$

Next, I saw that since the object is accelerating upward and parallel to the line connecting the two point charges, then q1 must be positive and q2 must be negative. Since Q is moving straight up, there is no movement in the x direction.

With that, I figured that:

$F = Fy$
$2.124 = 2 FQy$
$FQy = 1.062$

So far, I get that the total force is the vector sum of Fq1y and Fq2y. And since these vectors are in the y-direction, you can add their magnitudes (I think). I tried solving for q1 in Coulombs' law:

$F*r^2/kQ = q1$
$(1.062)(.03^2)/(8.99*10^9)(2*10^-6) = 5.3*10^-8 C$

(That should be 10^-6 but latex keeps putting the - sign up and not the 6. Not sure how to fix that but I calculated it correctly at that part)

But this isn't the right answer. I'm pretty sure that q1 and q2 have the same magnitude, just different charges (q1 is + and q2 is -), but I don't know what to do in order to find them. Any help would be appreciated. Thanks!

 

[TSny]

Hello, Ozmahn. Welcome to PF!

You stated correctly that you need to work with the y-components of the electric forces on Q. But in your calculations, I don't see where you actually worked with the y-component of either electric force on Q. Note that the given distances imply that Q cannot be located on the line connecting q₁ and q₂.

 

[Ozmahn]

Thanks TSny!

So I assumed that since Q is accelerating parallel to the line connecting q1 and q2, the sum of the y-components (Q1y and Q2y) is equivalent to the net force. I think the y-components of the vector from q1 to Q and q2 to Q are both equivalent in magnitude, just the charges themselves are opposite signs. And since they're y-components, their vectors are equivalent as well since q1 and q2 are at an equal distance from Q. So

$Fy=FQ1y+FQ2y=2FQy$
$2.124=2FQy$
$1.062=FQy$

And that 1.062 is the magnitude of the y-component of the vector created by q1 and q2. And since the y-component is the net force, then plugging that into Coulomb's law should solve it...at least, that's how I'm thinking about it but something is off. Am I looking at this the wrong way?

 

[TSny]

$Fy=FQ1y+FQ2y=2FQy$
$2.124=2FQy$
$1.062=FQy$

This looks good. However, be careful when you proceed to find q₁. Keep in mind that you are working with the y-component of the force.

 

[Ozmahn]

Ah okay, so just because both x-components cancel each other out, they still contribute to the force of their respective q's. So...I need to find the actual force of q1 and q2, not just its y-component? And I'm pretty sure I can do that with arcsin, and since the forces are equal in magnitude but have opposite charges. I'll try it out when I get home from class, thanks!

 

[TSny]

Just to make sure we're together. How would you write the expression for the magnitude of the force of q1 on Q? How would you then write the y-component of this force?

 

[Ozmahn]

Okay so here is what I did. I already knew what Q1y was (1.062), so I found the angle created by q1x and q1. To do this:

$tan\theta\\ = 0.0225/0.03 => arctan(0.0225/0.03) = 37$

So now that I know what the angle is, I can solve the smaller triangle created by q1, q1x, and q1y.

$sin\theta\ = q1y/q1 => q1 = q1y/sin\theta\ => 1.062/0.6 = 1.77 = q1$

Now that I know what force q1 is putting on Q, and I've already identified that q1 must be positive and q2 must be negative, I know their absolute value is 1.77 N. Now to find q1, I can use Coulomb's law:

$F = (k*Q*q1)/r^2$

Rewritten to solve for q1:

$q1= (F*r^2)/(k*Q)$
$q1= (1.77*0.03^2)/(8.99*10^9*2)$
$q1=8.86*10^-14$

And q2 would be the same, but negative. How does that sound?

 

[TSny]

Okay so here is what I did. I already knew what Q1y was (1.062), so I found the angle created by q1x and q1. To do this:

$tan\theta\\ = 0.0225/0.03 => arctan(0.0225/0.03) = 37$

I don't believe the tangent function is correct here. See diagram below.

So now that I know what the angle is, I can solve the smaller triangle created by q1, q1x, and q1y.

$sin\theta\ = q1y/q1 => q1 = q1y/sin\theta\ => 1.062/0.6 = 1.77 = q1$

Your notation is kind of dangerous. By q1 and q1y here, I guess you mean the forces F_q1Q and F_q1Q,y.

Now that I know what force q1 is putting on Q, and I've already identified that q1 must be positive and q2 must be negative, I know their absolute value is 1.77 N. Now to find q1, I can use Coulomb's law:

$F = (k*Q*q1)/r^2$

Rewritten to solve for q1:

$q1= (F*r^2)/(k*Q)$
$q1= (1.77*0.03^2)/(8.99*10^9*2)$
$q1=8.86*10^-14$

And q2 would be the same, but negative. How does that sound?

OK, but Q is not 2 Coulombs.

 

[Ozmahn]

I attached a picture of the system, this was provided by the website. I should have included that with the initial post, I didn't think it could be interpreted in the other direction.

Sorry about the notation, I should definitely be more clear about that. Yes, that is what I meant. I just realized how to format subscripts, so I'll start doing that with future posts.

Finally, it should be 2x10^-6 since it's in μC.

I think I got it this time...

 

[Ozmahn]

Ohh I see what you're saying. It shouldn't be tangent at all, I should be using opposite over hypotenuse. So sine instead.

The F_Qq1 comes out to 1.42 N, so plugging that into solve for q₁ I get 7.11x10^-8.

That was the correct answer. Thanks a lot for the help, I appreciate it!

 

[TSny]

Ok. Good work!